Chapter 2 Fluid Dynamics
“Stands on shifting sands, the scales held in her hands. The wind it just whips her and wails and fills up her brigantine sails.”
The Stone Roses, Waterfall (1989).
This chapter introduces fluid dynamics for CFD. It describes: governing equations, i.e. conservation of mass, momentum and energy; and, associated physical models, e.g. for viscosity, heat conduction and thermodynamics.
The equations describe fluid motion, forces and
heat in time and three-dimensional (3D) space. Vector notation
provides a mathematical framework to present the equations in a
compact form. It enables the equations to be presented
independently of any co-ordinate system, e.g. Cartesian (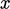 /
/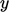 /
/ ) or spherical
(
) or spherical
( /
/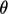 /
/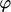 ). It includes a standard set of algebraic operations,
e.g. the inner (dot) and
outer products.
). It includes a standard set of algebraic operations,
e.g. the inner (dot) and
outer products.
The notation helps to ensure that the terms in equations are unchanged, or invariant, under a co-ordinate system transformation. Without invariance, a flow solution, e.g. along a pipe, would be dependent on the orientation of the pipe with respect to the co-ordinate system. Logically this dependence cannot exist; the laws of motion are the same in all “inertial frames”.1
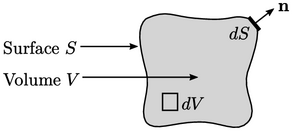
The derivation of the governing equations uses
a control volume 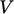 bounded by a surface
bounded by a surface  , presented using the
two-dimensional (2D)
illustration above. We use
, presented using the
two-dimensional (2D)
illustration above. We use  and
and 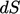 to describe an infinitesimally small volume
and surface, respectively, and
to describe an infinitesimally small volume
and surface, respectively, and 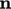 is the unit normal
vector for each increment of surface
is the unit normal
vector for each increment of surface  , discussed in
Sec. 2.1
. It is important to note in
any derivation whether the volume is defined as fixed in space or
moving with the fluid.
, discussed in
Sec. 2.1
. It is important to note in
any derivation whether the volume is defined as fixed in space or
moving with the fluid.
Each derivation generally begins with a definite
integral of some
quantity, e.g. 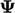 , over the
volume
, over the
volume  denoted by
denoted by
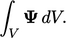 |
(2.1) |
 that make up the total
volume
that make up the total
volume 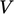 . The summed values are
. The summed values are 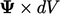 , where
, where  is the value in the
respective
is the value in the
respective  .
.
The derivations also use integrals over the
surface 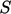 , e.g.
, e.g.
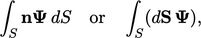 |
(2.2) |
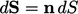 . Volume and surface integrals are connected through Gauss’s
Theorem, introduced in Sec. 2.4
.
. Volume and surface integrals are connected through Gauss’s
Theorem, introduced in Sec. 2.4
.
2.2 Velocity
2.3 Flow through a surface
2.4 Conservation of mass
2.5 Time derivatives
2.6 Forces at a surface
2.7 Conservation of momentum
2.8 Flow in a volume
2.9 Conservation and boundedness
2.10 Fluid deformation
2.11 Vorticity
2.12 Newtonian fluid
2.13 Incompressible flow
2.14 Diffusion
2.15 Conservation of energy
2.16 Temperature
2.17 Internal energy
2.18 Heat capacity
2.19 Energy and temperature
2.20 Natural convection
2.21 Scale similarity
2.22 Region of influence
2.23 Summary of equations
2.24 Summary of tensor algebra
2.25 Vector identities

