2.21 Scale similarity
Scale similarity is the notion that, for two systems that are geometrically similar, the flow will follow the same path if the ratio of magnitude of forces acting on the fluid is the same at different points in the flow.
Flows at different scales can be compared using dimensionless variables. The momentum equation, Eq. (2.67 ), with advection, diffusion and gravity forces can be expressed in non-dimensionalised form by
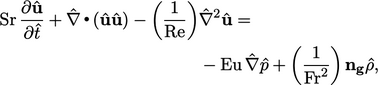 |
(2.68) |
- Strouhal number
 — transient/steady inertia;
— transient/steady inertia; - Reynolds number
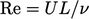 — inertia/viscous force;
— inertia/viscous force; - Euler number
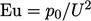 — pressure force/inertia;
— pressure force/inertia; - (Froude number)

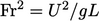 — inertia/gravity
force.
— inertia/gravity
force.
These dimensionless numbers include a
characteristic length 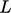 , time
, time 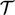 , speed
, speed 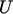 and pressure
and pressure
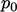 .
The
.
The  (hat) notation indicates dimensionless length, time, etc., e.g.
(hat) notation indicates dimensionless length, time, etc., e.g. 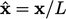 and
and 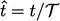 and corresponding
dimensionless operators
and corresponding
dimensionless operators  and
and 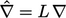 .
.
Equation 2.68
assumes constant
 and
splits gravitational acceleration
and
splits gravitational acceleration 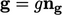 into its magnitude
into its magnitude
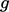 and
unit direction
and
unit direction 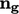 ; pressure, including
; pressure, including 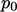 , is in kinematic units
(divided by
, is in kinematic units
(divided by 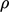 ).
).
The dimensionless numbers provide a comparison of
the magnitudes of different fluid forces. For example, 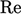 represents the
ratio of inertia force to viscous force and plays a pivotal role in
turbulence modelling, introduced in Chapter 6
.
represents the
ratio of inertia force to viscous force and plays a pivotal role in
turbulence modelling, introduced in Chapter 6
.
Scale similarity applies also to other
transported properties. For example, the energy equation,
Eq. (2.65
),
ignoring heat sources  , can be expressed in non-dimensional form
as
, can be expressed in non-dimensional form
as
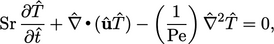 |
(2.69) |
Again in Eq. (2.69
), the  (hat) notation
is applied to temperature
(hat) notation
is applied to temperature 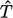 to indicate a dimensionless temperature,
although it notably does not appear in a dimensionless number.
to indicate a dimensionless temperature,
although it notably does not appear in a dimensionless number.
In fact, with the exception of momentum (which
uses 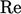 ),
),  represents more generally the rates of advection and
diffusion, as a ratio, for any transported quantity (here, it is
heat).
represents more generally the rates of advection and
diffusion, as a ratio, for any transported quantity (here, it is
heat).
Further numbers23 define the ratios of diffusivities, e.g.:
where 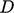 is mass diffusivity (not discussed in this
book).
is mass diffusivity (not discussed in this
book).
Dimensionless numbers can be multiplied and
divided with one another to form further dimensionless numbers. For
example, the Péclet number for heat transfer 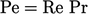 .
.

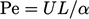 — advection/diffusion of heat.
— advection/diffusion of heat.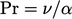 — viscosity/thermal diffusivity;
— viscosity/thermal diffusivity;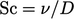 — viscosity/mass diffusivity.
— viscosity/mass diffusivity.