Notes on Computational Fluid Dynamics: General Principles

2.11 Vorticity

Vorticity describes the tendency for a fluid to rotate locally, defined as

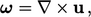(2.37)

where the operator is the curl derivative. The curl of a vector 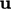is evaluated in Cartesian co-ordinates by

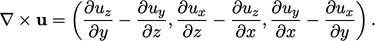(2.38)

The local rotation which vorticity measures is not due to the flow following a curved path. In fact, vorticity is often associated with shear when streamlines may be straight and parallel, i.e. not curved at all.

Vorticity is difficult to picture under shear because the deformation masks the local rotation. By separating the deformation, as in the figure in Sec. 2.10 , the local rotation is revealed.

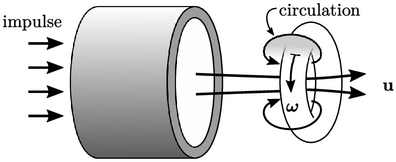
Vorticity is often demonstrated by a vortex ring produced by an air “cannon” with smoke to visualise the flow. It reveals flow circulation around sections of the torus, from front to back. The vorticity vectors are normal to the planes of circulation, along the axis of the torus.

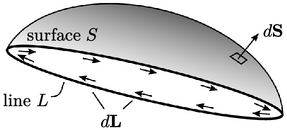
Stokes’s theorem⁸ relates circulation — the integral of 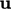around a closed curved line, 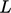— to the integral of vorticity 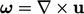over a section of surface 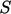bounded by the curve, according to:

(2.39)

In Eq. (2.39 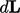), is a vector representing a segment of the line 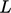. As you stand on 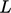looking in the direction , with your head in the direction 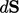, is oriented to your left.

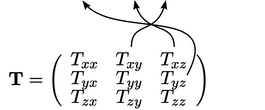
Vorticity is related to the spin tensor in Eq. (2.33 ) by 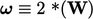, where 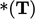is the Hodge dual operator which extracts components of a vector from a tensor as shown below:

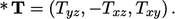(2.40)

The term “spin tensor” emphasises local rotation as opposed to the general path in a similar way that the spin on a ball is clearly distinguished from its trajectory, which curves due to gravity.

---

---