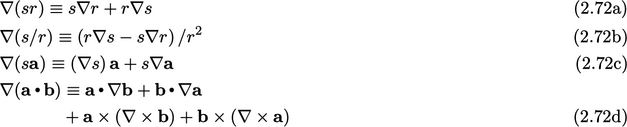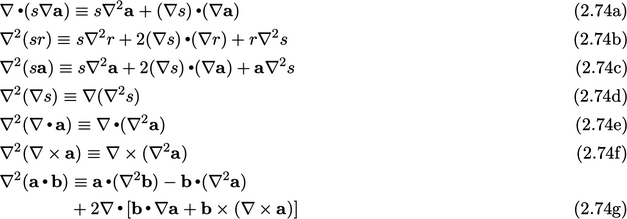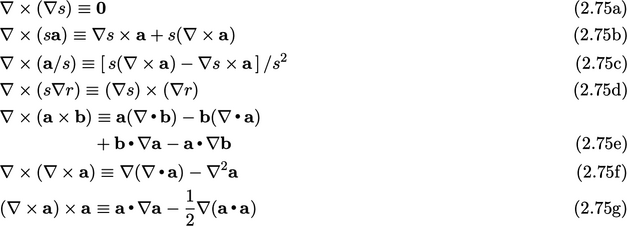2.25 Vector identities
Several identities are listed below which can
be verified under the assumption that the relevant derivatives exist
and are continuous. The identities are expressed for: scalars
 ,
,
 ;
vectors
;
vectors 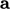 ,
, 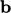 ,
,  ; tensor
; tensor 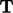 .
.
Algebraic operations
Gradient derivatives
Divergence derivatives
Laplacian derivatives
Curl derivatives
Notes on CFD: General Principles - 2.25 Vector identities