Notes on Computational Fluid Dynamics: General Principles

2.20 Natural convection

In Sec. 2.13 , a set of equations — Eq. (2.47 ) and Eq. (2.48 ) — was derived for flow of an incompressible fluid. They are a sample set of equations for mass and momentum conservation that can be solved using methods described in this book.

The example set of equations can be extended to include energy conservation and associated models of heat conduction and heat capacity, described in Sec. 2.15  - 2.18 .

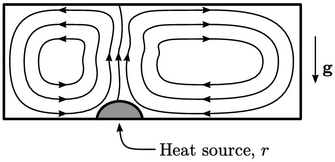
The set of equations for mass, momentum and energy can be combined to simulate natural convection, e.g. for flow of air around a room. In natural convection, a non-uniform temperature causes density variations which generate associated forces due to gravity. Colder air is driven downwards and hot air rises, creating buoyancy. Small temperature variations, e.g. due to a heat source , can cause buoyancy to be the dominant force.

A simple, approximate equation for 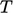can be derived, starting from internal energy conservation in the form of Eq. (2.57 ). The approximations of constant 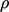(with 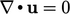) and zero viscosity reduce the stress/pressure work terms to zero.

Assumin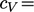g  constant, we can apply Eq. (2.63 ), which reduces to substituting by since derivatives of constants and 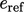are zero. Applying Fourier’s law Eq. (2.54) leads to

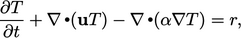(2.65)

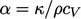where thermal diffusivity and becomes a thermal source in SI units of .

This is another example, similar to Eq. (2.49 ), of a transport equation containing a time derivative, advection, diffusion and a source of heat. Applying suitable boundary conditions, the equation can be solved for .

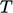Buoyancy force

The effect of buoyancy can be simulated by setting the body force 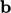in Eq. (2.47 ) for an incompressible, Newtonian fluid. While the assumption 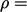 constant is applied across all the governing equations generally, it cannot be applied to this force. Therefore we apply

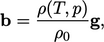(2.66)

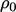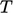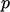where is a density at a reference state, e.g. at the initial and , and 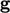is the acceleration due to gravity.

The density 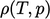is a function of 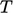and, optionally, 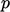provided by some equation of state, e.g. the ideal gas Eq. (2.55 ). The final momentum equation including this buoyancy force, and assuming 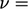 constant is:

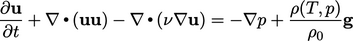(2.67)

The combined set of equations for mass, momentum and energy becomes Eq. (2.48 ) Eq. (2.67 ) and Eq. (2.65 ) respectively, which can be used to solve flows with natural convection.