2.16 Temperature
In the conservation of energy
Eq. (2.51
), the mechanical kinetic energy,
power flux and sources can be calculated from 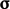 ,
, 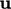 and
and 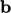 from the momentum
Eq. (2.19
). Heat sources can contribute
to
from the momentum
Eq. (2.19
). Heat sources can contribute
to  ,
e.g. from thermal
radiation, chemical reactions etc.
,
e.g. from thermal
radiation, chemical reactions etc.
That leaves the heat flux term 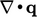 which represents
conduction of heat. It is commonly modelled by Fourier’s
law14
which states
which represents
conduction of heat. It is commonly modelled by Fourier’s
law14
which states  is proportional to the negative gradient of
temperature
is proportional to the negative gradient of
temperature 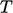 , i.e.
, i.e.
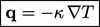 |
(2.54) |
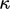 .
.
Temperature scale
The heat flux Eq. (2.54) requires temperature to be defined and measurable. Measurement requires a scale. Empirical scales correlate temperature with a measured physical property of a working substance, e.g. EMF at a junction of two metal alloys. Empirical scales have the drawbacks of: being dependent on the working substance; and, not actually defining temperature.
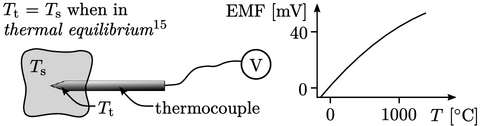
Instead, the thermodynamic scale defines temperature
as a measure of the average kinetic energy of random motions of
particle constituents of matter. It provides an absolute measure of temperature that is
independent of the choice of working substance and includes a zero
point16. It
must be measured in units with a zero point, such as the SI unit
Kelvin, 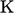 .
.
Substitution of our model Eq. (2.54) into
Eq. (2.51
) yields the term 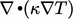 . It is logical that
this is a Laplacian term since it represents diffusion which is
associated with random motions of submicroscopic particles, as we
we established in Sec. 2.14
.
. It is logical that
this is a Laplacian term since it represents diffusion which is
associated with random motions of submicroscopic particles, as we
we established in Sec. 2.14
.
Ideal gas
The behaviour of many gases under typical working conditions is captured by the ideal gas equation of state
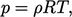 |
(2.55) |
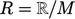 .
It is calculated from the Universal Gas Constant
.
It is calculated from the Universal Gas Constant 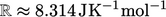 in SI units, and the
molar mass
in SI units, and the
molar mass 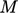 of the gas,
with units of
of the gas,
with units of 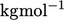 .
.
The ideal gas equation originates from classical thermodynamics as a combination of empirical laws17. Later, it was derived from first principles from both statistical thermodynamics and kinetic theory, with temperature representing average kinetic energy.
The derivations assume that molecules have no volume, undergo purely elastic collisions and there are no inter-molecular forces.
A scale of temperature defined by the ideal gas equation of state is exactly equivalent to the thermodynamic temperature scale.

