2.19 Energy and temperature
Specific internal energy  and temperature
and temperature
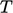 were described in Sec. 2.17
and Sec. 2.16
, respectively. They are
related through the specific heat capacity
were described in Sec. 2.17
and Sec. 2.16
, respectively. They are
related through the specific heat capacity 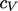 , defined by
Eq. (2.61
) in Sec. 2.18
.
, defined by
Eq. (2.61
) in Sec. 2.18
.
Analyses involving heat usually incorporate both
 and
and
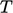 since:
since:
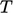 is the measurable quantity specified as initial
and boundary data and whose data is required as part of the
“results”;
is the measurable quantity specified as initial
and boundary data and whose data is required as part of the
“results”; is the calculated quantity solved in energy
conservation, e.g.
Eq. (2.51
), but whose data is usually of no
interest.
is the calculated quantity solved in energy
conservation, e.g.
Eq. (2.51
), but whose data is usually of no
interest.
Conversion of values between  and
and 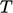 is therefore
needed, and vice versa. Incorporating Eq. (2.61
) into a definite integral for
is therefore
needed, and vice versa. Incorporating Eq. (2.61
) into a definite integral for
 ,
,
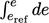 ,
gives
,
gives
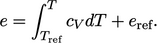 |
(2.62) |
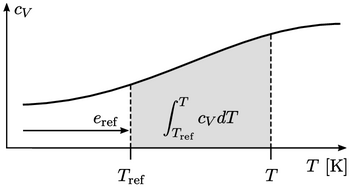
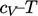 graph. Energy
graph. Energy  is represented by the area under the curve, in which
is represented by the area under the curve, in which
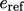 represents a
reference energy up to a reference temperature
represents a
reference energy up to a reference temperature 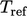 , and the integral from
, and the integral from
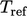 to
to
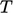 is
shown by the shaded area.
is
shown by the shaded area.
For applications that cover a reasonably narrow
temperature range, 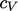 can be assumed constant. From
Eq. (2.62
), the
can be assumed constant. From
Eq. (2.62
), the 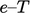 relation becomes
relation becomes
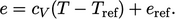 |
(2.63) |
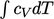 can be integrated analytically by representing
can be integrated analytically by representing
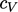 by
a polynomial of order
by
a polynomial of order 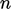 with coefficients
with coefficients 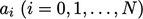 fitted to measured
fitted to measured
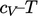 data
data
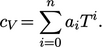 |
(2.64) |
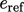 and
and 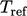 ultimately add a constant component to
ultimately add a constant component to  . Since
Eq. (2.51
) is concerned with changes in
. Since
Eq. (2.51
) is concerned with changes in  and the absolute values
and the absolute values
 are
usually of no interest, the values of
are
usually of no interest, the values of 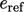 and
and 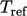 are often
immaterial.
are often
immaterial.
The 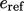 and
and 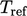 values become important when the
composition of a fluid changes due to the mixing of constituent fluid
species, e.g.
values become important when the
composition of a fluid changes due to the mixing of constituent fluid
species, e.g. 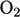 ,
, 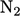 , or chemical
reactions, e.g. with
, or chemical
reactions, e.g. with
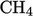 .
Each fluid specie possesses a different
.
Each fluid specie possesses a different 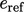 so any change to the
specie concentrations will change
so any change to the
specie concentrations will change  of the overall fluid.
of the overall fluid.
In those circumstances, 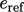 is commonly represented
by the heat
of formation per unit mass,
is commonly represented
by the heat
of formation per unit mass, 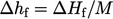 . The standard heat of formation
. The standard heat of formation 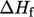 is the change
of enthalpy during the formation of 1 mole of a substance from its
constituent elements at standard temperature
is the change
of enthalpy during the formation of 1 mole of a substance from its
constituent elements at standard temperature 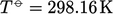 . Measured heats of
formation are available for numerous fluid species.20
. Measured heats of
formation are available for numerous fluid species.20
If an analysis involves changes to fluid
composition, it can then adopt 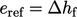 and
and 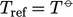 for individual fluid
species, to account for the change in
for individual fluid
species, to account for the change in  due to changes in the
concentrations of fluid species.
due to changes in the
concentrations of fluid species.

