2.4 Conservation of mass
The law of conservation of mass can be written
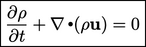 |
(2.8) |
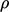 is the mass density of the fluid. The equation can be
derived by considering a volume
is the mass density of the fluid. The equation can be
derived by considering a volume 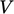 fixed in space (note !!), bounded by a
surface
fixed in space (note !!), bounded by a
surface 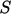 . If the volume is filled by a fluid with density
. If the volume is filled by a fluid with density 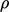 , its mass is
, its mass is
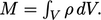
The rate of increase of mass inside the volume
must match the rate of inflow of mass across the volume’s surface.
The latter is calculated by integrating the mass flux  over the surface, noting
the negative sign due to
over the surface, noting
the negative sign due to 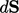 pointing out of the volume.
pointing out of the volume.

Gauss’s Theorem relates surface and volume integrals by
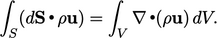 |
(2.9) |
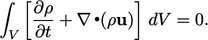 |
(2.10) |
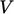 , it follows that the
integrand (in
, it follows that the
integrand (in  ) must equal 0, resulting in Eq. (2.8).
) must equal 0, resulting in Eq. (2.8).
Divergence
Divergence, denoted by  , indicates the tendency
of a vector field to point outward of a closed surface. For example,
When the divergence of velocity
, indicates the tendency
of a vector field to point outward of a closed surface. For example,
When the divergence of velocity 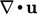 is positive, the fluid
is expanding; negative divergence indicates contraction. Imagine a
volume of fluid with a complex distribution of
is positive, the fluid
is expanding; negative divergence indicates contraction. Imagine a
volume of fluid with a complex distribution of 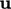 at its bounding
surface, below left. The
at its bounding
surface, below left. The 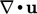 calculation will isolate the diverging
component (right) from uniform flow (centre).
calculation will isolate the diverging
component (right) from uniform flow (centre).
The divergence of velocity is calculated by
integrating — i.e. summing
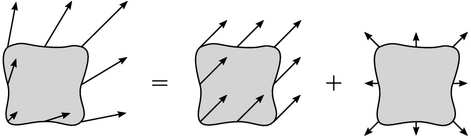
— fluxes over the closed surface. To define divergence at a point, we consider the limiting
case where the volume tends to zero. For a surface 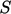 that encloses a
volume
that encloses a
volume 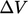 , divergence is the flux across the
surface per unit volume, as
, divergence is the flux across the
surface per unit volume, as  , e.g.
, e.g.
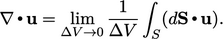 |
(2.11) |
The nabla operator
The nabla symbol 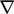 can be considered a
vector operator
can be considered a
vector operator
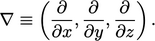 |
(2.12) |
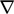 , e.g.
, e.g.
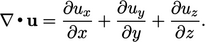 |
(2.13) |

