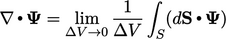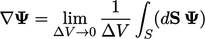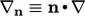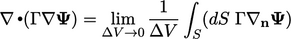2.23 Summary of equations
- Force
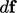 at
a surface:
at
a surface:

- Rate of
deformation
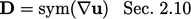
Conservation laws
Constitutive models
- Newtonian
fluid, Sec. 2.12
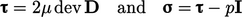
- Fourier’s
law, Sec. 2.16
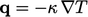
- Ideal
gas, Sec. 2.16
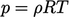
- Specific heat
capacity, Sec. 2.18
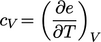
- Energy-temperature relation,
Sec. 2.19
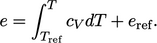
Derivatives
Notes on CFD: General Principles - 2.23 Summary of equations

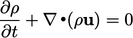
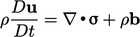

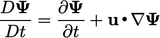
 is vector, tensor
is vector, tensor