2.14 Diffusion
The momentum equation for a homogeneous,
incompressible, Newtonian fluid is presented in Eq. (2.47
). In the case of
zero body force, 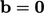 , and
, and 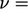 constant, Eq. (2.47
) becomes
constant, Eq. (2.47
) becomes
 |
(2.49) |
- the local rate of change
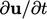 , described in
Sec. 2.5
;
, described in
Sec. 2.5
; - advection of
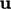 by
by 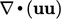 , described in
Sec. 2.8
;
, described in
Sec. 2.8
; - diffusion of
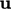 by
by 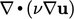 ;
; - a “source” due to
 , described in
Sec. 2.12
.
, described in
Sec. 2.12
.
Note that, since 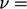 constant,
constant,
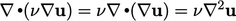 ,
where
,
where 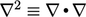 denotes the Laplace operator.
denotes the Laplace operator.
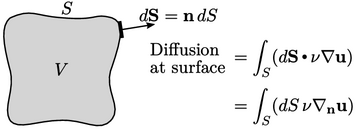
The 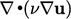 term is a special form of divergence in which
the flux includes the surface normal gradient denoted by the operator
term is a special form of divergence in which
the flux includes the surface normal gradient denoted by the operator
 where
where 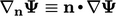 .
.
The term models diffusion across the surface of the fluid
element. Diffusion generally represents the transport of a fluid
property — here, momentum — due to fluctuating motions that are not
captured by the bulk motion that is represented by the continuum velocity 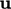 .
.
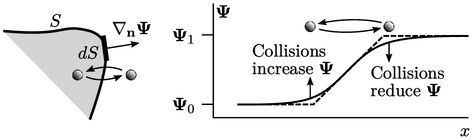
Fluctuations include any random motion of
particle constituents of matter, e.g. molecules, and turbulent
structures. Through these motions, particles can pass across a
surface boundary, transporting property 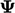 through a gradient of
through a gradient of
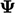 (above, left).
(above, left).
Particles carrying higher 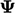 move into regions of
particles with lower
move into regions of
particles with lower 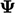 and vice versa. Through particle collisions,
high values of
and vice versa. Through particle collisions,
high values of 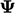 tend to reduce and low values increase (right).
tend to reduce and low values increase (right).
Laplacian
“Laplacian”11 describes a term of the form 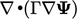 where
where  is a diffusivity
coefficient.12 A
Laplacian term is conservative since all variables are to
the right of a divergence, as described in Sec. 2.9
. It is also bounded since it tends to decrease high
values and increase low values as shown above.
is a diffusivity
coefficient.12 A
Laplacian term is conservative since all variables are to
the right of a divergence, as described in Sec. 2.9
. It is also bounded since it tends to decrease high
values and increase low values as shown above.
The Laplacian represents a flux due to
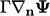 across the surface, per unit volume, as
across the surface, per unit volume, as 
 |
(2.50) |
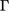 , i.e.
, i.e.
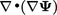 , represented as
, represented as 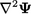 but we include
but we include
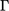 here because it is generally
needed.
here because it is generally
needed.
