Notes on Computational Fluid Dynamics: General Principles

2.5 Time derivatives

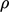The conservation of mass Eq. (2.8 ) included a partial derivative in time relating to a fixed region of space. This is the local rate of change of , relating to the change in 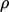in the fluid measured by an observer at a fixed location. It is not the time rate of change experienced by a mass of fluid particles as they move through space. In the same way, 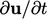is not the acceleration experienced by the fluid.

Acceleration relates to the material, or substantive, derivative which describes the time rate of change of a fixed mass of moving material. It is denoted by 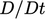and is related to the local rate of change, using as an example tensor of any rank, by

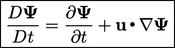(2.14)

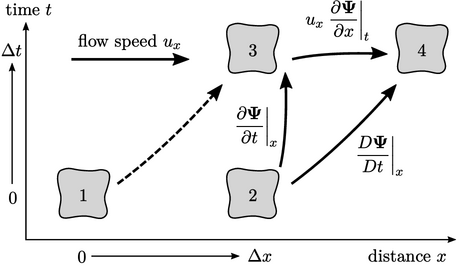
The relation is derived from the chain rule of differential. In one dimension, it is illustrated by two particles of fluid that occupy positions 1 and 2 at some initial time, then positions 3 and 4 at a later time . The particles move in the -direction at speed 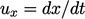, such that the particle at 1 later occupies the position 3 and the particle at 2 occupies position 4.

The material time derivative of , following the mass from 24, is the sum of: the local change in 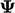at a fixed position (23); and, the change due to the gradient of 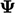 between positions 3 and 4, fixing time 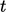. This equates to

(2.15)

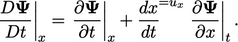The material derivative relation in Eq. (2.14) is simply the 3D equivalent of Eq. (2.15 ).

Gradient

The last term in Eq. (2.14) introduces the gradient denoted by . If 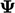is a scalar, the gradient produces a vector whose magnitude and direction is that of the steepest gradient.

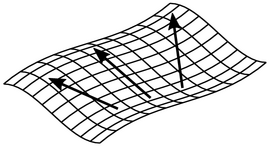
The figure above illustrates the gradient using a surface that represents a distribution of a scalar field in 2 directions. The gradients at 3 locations are in the direction of steepest ascent.

When 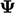is a vector, the gradient produces a tensor, representing the direction and magnitude of steepest ascent for each of the 3 components of the vector.