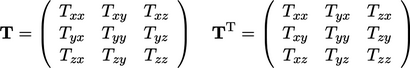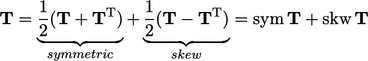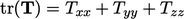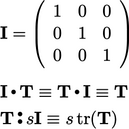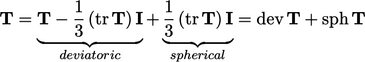2.24 Summary of tensor algebra
Below is tensor algebra applied to Cartesian
(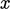 ,
, 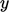 ,
,  ) co-ordinates using: scalar
) co-ordinates using: scalar  ; vectors
; vectors
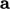 ,
,
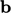 ;
tensors
;
tensors 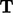 ,
, 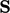 ,
, 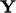 .
.
Products
- Inner product
of two vectors, Sec. 2.3
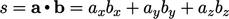
- Outer product
of two vectors, Sec. 2.8
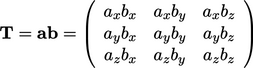
- Inner product
of vector and tensor, Sec. 2.6
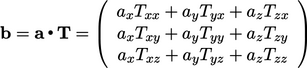
- Inner product
of two tensors, Sec. 2.8
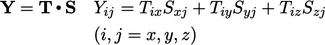
- Double inner
product of two tensors, Sec. 2.17
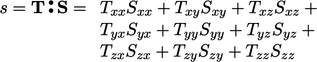
- Cross product
of two vectors, first used in Sec. 3.3
, produces a vector with
components
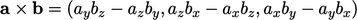
(2.70)
Tensors and operations
Notes on CFD: General Principles - 2.24 Summary of tensor algebra