2.7 Conservation of momentum
The law of conservation of momentum can be
written

|
(2.19) |
where
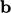
represents any body force
per unit mass. Body forces represent any force
which does not act at a bounding surface, including those that act
at a distance, such as gravitational force.
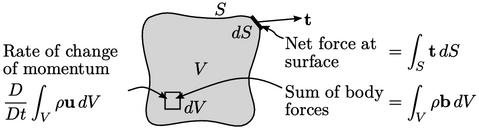
The equation is derived by considering the time
rate of change of the momentum of a mass of particles. We consider
a volume of material of fixed
mass moving through space and therefore present rate of
change by the material derivative 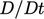 .
.
Applying Gauss’s theorem
and Eq. (2.16
), the surface force is
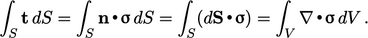
|
(2.20) |
Equating the rate of change of momentum to the forces and, noting
mass is fixed so
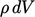
is constant in time, gives
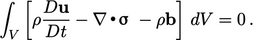
|
(2.21) |
The integrand must equal 0, resulting in Eq. (
2.19).
Divergence was described in section 2.4
as the flux across a surface per
unit volume as 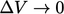 . The divergence of stress
similarly represents the stress flux across the surface,
i.e. force, per unit volume
as
. The divergence of stress
similarly represents the stress flux across the surface,
i.e. force, per unit volume
as 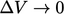 ,
given by
,
given by

|
(2.22) |
Eq. (
2.19
) specifically relates to
linear momentum. Instead,
conservation of
angular
momentum
, in the absence of any “couple stresses” that
generate a moment field, is given by
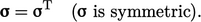
|
(2.23) |
The derivation of Eq. (
2.23
) is fairly complex so is
omitted here.
Tensor symmetry
Symmetry in a tensor 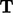 refers to components
being symmetric about the diagonal, i.e.
refers to components
being symmetric about the diagonal, i.e. 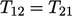 ,
, 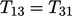 and
and 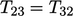 . The transpose of a tensor, denoted by the
‘
. The transpose of a tensor, denoted by the
‘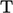 ’
superscript, switches components across the diagonal such that:
’
superscript, switches components across the diagonal such that:
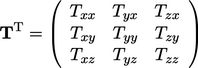
|
(2.24) |
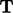
is
therefore
symmetric if
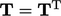
. A
skew (anti-symmetric) tensor has
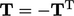
. A tensor can be
decomposed into symmetric and skew parts by:

|
(2.25) |

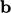 represents any body force per unit mass. Body forces represent any force
which does not act at a bounding surface, including those that act
at a distance, such as gravitational force.
represents any body force per unit mass. Body forces represent any force
which does not act at a bounding surface, including those that act
at a distance, such as gravitational force.
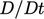 .
.
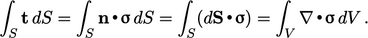
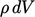 is constant in time, gives
is constant in time, gives
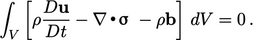
 . The divergence of stress
similarly represents the stress flux across the surface,
i.e. force, per unit volume
as
. The divergence of stress
similarly represents the stress flux across the surface,
i.e. force, per unit volume
as 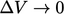 ,
given by
,
given by
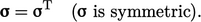
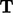 refers to components
being symmetric about the diagonal, i.e.
refers to components
being symmetric about the diagonal, i.e. 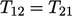 ,
, 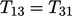 and
and 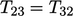 . The transpose of a tensor, denoted by the
‘
. The transpose of a tensor, denoted by the
‘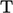 ’
superscript, switches components across the diagonal such that:
’
superscript, switches components across the diagonal such that: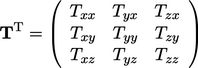
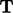 is
therefore symmetric if
is
therefore symmetric if 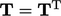 . A skew (anti-symmetric) tensor has
. A skew (anti-symmetric) tensor has 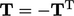 . A tensor can be
decomposed into symmetric and skew parts by:
. A tensor can be
decomposed into symmetric and skew parts by:


