2.2 Velocity
Like force, velocity 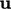 is a vector with
direction and magnitude, with SI units of
is a vector with
direction and magnitude, with SI units of  . Using the vector
. Using the vector
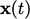 to
denote the position of a particle of fluid, its velocity is
to
denote the position of a particle of fluid, its velocity is
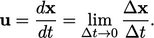 |
(2.4) |
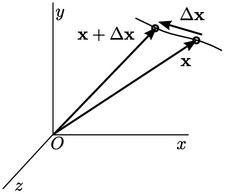
Vector fields
While 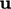 can be used to denote a single velocity
with magnitude and direction, it can also denote a vector field of velocity which varies
from point to point across a spatial domain. A vector is
represented by 3 numbers, relating to the co-ordinate system being
used, e.g.
can be used to denote a single velocity
with magnitude and direction, it can also denote a vector field of velocity which varies
from point to point across a spatial domain. A vector is
represented by 3 numbers, relating to the co-ordinate system being
used, e.g. 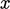 ,
, 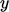 ,
,  , in the Cartesian
system.
, in the Cartesian
system.
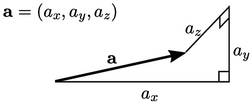
While the magnitude and direction of a vector is
fixed, it is not invariant since the 3 values depend on the co-ordinate system
used. We represent a vector without reference to the co-ordinate
system by bold text, e.g.
“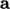 ”
(compared to scalar “
”
(compared to scalar “ ”).
”).
Basic vector algebra
Addition and subtraction of 2 vectors is performed by operating
on respective components. Subtraction of two vectors 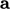 and
and
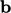 is
performed by
is
performed by
 |
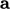 by a scalar
by a scalar
 is
performed by multiplying all the components by the scalar,
e.g.
is
performed by multiplying all the components by the scalar,
e.g.
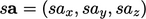 |
 ). Subtraction is not commutative. Products between scalars
and vectors are distributive,
i.e.
). Subtraction is not commutative. Products between scalars
and vectors are distributive,
i.e.
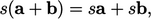 |
 ,
,
 |
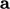 and a scalar is
only relevant when the scalar is the second argument of the
operation, i.e.
and a scalar is
only relevant when the scalar is the second argument of the
operation, i.e.
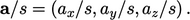 |

