2.8 Flow in a volume
We presented conservation of momentum,
Eq. (2.19
), in terms of the material
derivative 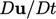 . To solve the equation in this form, would require a method
that tracks particles of fluid as they move around.
. To solve the equation in this form, would require a method
that tracks particles of fluid as they move around.
Generally it is easier to solve the equation by
fixing the volume of space
and solving for the fluid motion through it. To enable this, we
replace the material derivative for 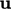 using the following
expression:
using the following
expression:
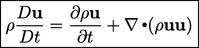 |
(2.26) |

Conservation of momentum can then be written
 |
(2.27) |
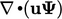 or
or  represents the bulk motion of the fluid at
velocity
represents the bulk motion of the fluid at
velocity 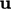 , which transports the property
, which transports the property 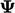 (a tensor of any rank)
by advection6. For example, if the property
(a tensor of any rank)
by advection6. For example, if the property 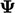 is temperature,
then advection will transport heat from one region of the flow
domain to another.
is temperature,
then advection will transport heat from one region of the flow
domain to another.
Advection contains a divergence derivative so
represents a flux across a surface per unit
volume. The example in Eq. (2.27
) represents the flux of
momentum, where the advected property is itself 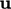 (or
(or 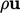 , depending whether
, depending whether
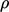 is
associated with bulk flow or the advected property).
is
associated with bulk flow or the advected property).
Outer product of two vectors
The advection term in Eq. (2.27)
includes a product of two vectors 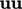 . This is the outer
product of two vectors7 which produces a tensor by
. This is the outer
product of two vectors7 which produces a tensor by
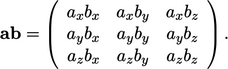 |
(2.28) |
Inner product of two tensors
The inner product of two tensors, e.g.  produces a tensor
produces a tensor
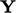 where the components are (replacing
where the components are (replacing 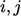 with
with 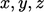 )
)
 |
(2.29) |
Identity tensor
The identity tensor 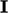 is the tensor
equivalent of unity (one) such that for any tensor
is the tensor
equivalent of unity (one) such that for any tensor 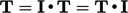 ,
,
 |
(2.30) |
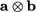 ”, but we write it as a product with no symbol, similar
to a scalar multiplication.
”, but we write it as a product with no symbol, similar
to a scalar multiplication.
