2.15 Conservation of energy
The law of conservation of energy13 states that the total energy of an isolated system remains constant over time. Energy is not created or destroyed, but is transformed from one form to another. If we consider mechanical and thermal energy, it can be expressed by
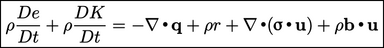 |
(2.51) |
 , where specific denotes per unit mass. Mechanical energy is
represented by specific kinetic energy
, where specific denotes per unit mass. Mechanical energy is
represented by specific kinetic energy 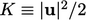 .
.
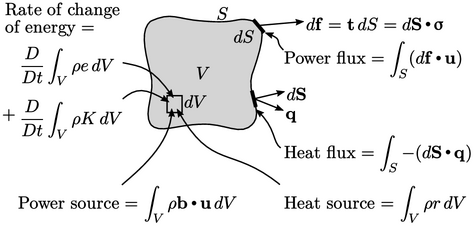
The rate of change of these combined energies is due to the input of mechanical power and heat from both surface fluxes and internal sources.
Mechanical power is
calculated by the inner product of force and 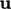 . The power over a
surface segment
. The power over a
surface segment 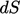 is
is 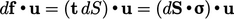 , representing a change in strain energy. The
internal power source is
, representing a change in strain energy. The
internal power source is 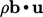 , representing a
change in potential energy due to general body forces.
, representing a
change in potential energy due to general body forces.
Heat is provided by an internal source of
strength  per unit mass and a surface heat
per unit mass and a surface heat
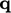 per unit
surface area. The surface heat flux relating to heat input takes a negative sign,
per unit
surface area. The surface heat flux relating to heat input takes a negative sign,
 ,
since
,
since 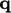 follows the convention of pointing out of the volume.
follows the convention of pointing out of the volume.
Equation 2.51
is derived by equating integrals
of rate of change of energy to the mechanical power and heat input
and taking  inside the volume integral since
inside the volume integral since 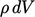 is constant in time, as
follows:
is constant in time, as
follows:
![Z De- + DK-- dV = V Dt Dt Z Z [ dS q + (dS ☐☐☐) u] + [ r + b u] dV: S V \relax \special {t4ht=](img/index663x.png) |
(2.52) |
![Z [ r q + r (☐☐☐ u)] dV: V \relax \special {t4ht=](img/index664x.png) |
(2.53) |

