2.17 Internal energy
The conservation of energy Eq. (2.51
) introduces the internal energy
using the specific quantity  , measured in
, measured in 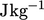 in SI units. It
represents the total molecular energy consisting of: kinetic energy
associated with temperature; potential energy due to particle
forces, both within
particles as chemical bonds, and between particles, e.g. van der Waals forces.
in SI units. It
represents the total molecular energy consisting of: kinetic energy
associated with temperature; potential energy due to particle
forces, both within
particles as chemical bonds, and between particles, e.g. van der Waals forces.
The energies at different scales can be summarised as:
- bulk — kinetic
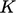 due to bulk motion,
potential due to forces
due to bulk motion,
potential due to forces  and
and 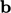 ;
; - molecular — kinetic characterised by
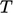 ,
potential due to bonds.
,
potential due to bonds.
To understand how energy is transferred between
these scales, we can derive an equation for internal energy from
Eq. (2.51
), by cancelling terms in
mechanical energy formed by taking the inner product of
Eq. (2.19
) with 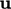 .
.
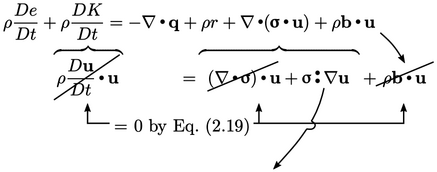
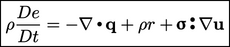 |
(2.56) |
The identity  is the key element of
the analysis. The
is the key element of
the analysis. The 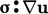 term in Eq. (2.56
) must represent the
contribution of mechanical power to the internal energy,
i.e. passing from bulk to
molecular scale. Conversely, the
term in Eq. (2.56
) must represent the
contribution of mechanical power to the internal energy,
i.e. passing from bulk to
molecular scale. Conversely, the 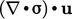 term must contribute to
mechanical energy.
term must contribute to
mechanical energy.
Substituting 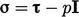 from Eq. (2.41
), Eq. (2.56)
becomes
from Eq. (2.41
), Eq. (2.56)
becomes
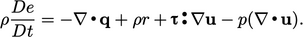 |
(2.57) |
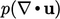 depends on
depends on 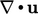 , i.e. whether the fluid is expanding or
contracting. Since the sign can change, it therefore represents a
recoverable contribution to
internal energy.
, i.e. whether the fluid is expanding or
contracting. Since the sign can change, it therefore represents a
recoverable contribution to
internal energy.
If we substitute the Newtonian model from Eq. (2.41 )
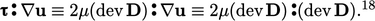 |
(2.58) |
 term is always positive
since all components of
term is always positive
since all components of 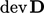 are squared. Its contribution to
are squared. Its contribution to
 is
therefore non-recoverable
and represents mechanical power that is dissipated as heat. In the
majority of CFD analyses, the
is
therefore non-recoverable
and represents mechanical power that is dissipated as heat. In the
majority of CFD analyses, the 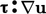 contribution is small
and can be ignored.
contribution is small
and can be ignored.
Double inner product of two tensors
The double inner product of two tensors,
denoted by “ ”, is introduced in Eq. (2.56). It
produces a scalar which is evaluated as the sum of the 9 products
of the tensor components, eg:
”, is introduced in Eq. (2.56). It
produces a scalar which is evaluated as the sum of the 9 products
of the tensor components, eg:
 |
(2.59) |
 ,
, 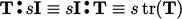 .
.
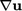 by
by  which is equivalent due
to symmetry of
which is equivalent due
to symmetry of  .
. 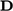 can then be replaced by
can then be replaced by 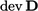 since
since 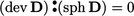 .
.
