2.22 Region of influence
A CFD calculation is performed by solving partial differential equations, such e.g. for conservation of mass, momentum and energy, over a solution domain. It requires suitable boundary conditions, discussed in Chapter 4 .
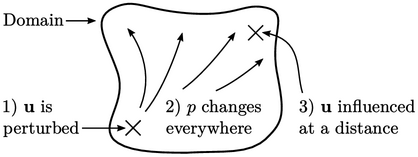
The solution is influenced by any change in a field
value, e.g.  ,
,  ,
,  , at some point in
the domain, e.g. at an
inlet boundary. The form of the equation determines the way in
which these changes, or perturbations, propagate across the
domain over time.
, at some point in
the domain, e.g. at an
inlet boundary. The form of the equation determines the way in
which these changes, or perturbations, propagate across the
domain over time.
Momentum and mass conservation for an
incompressible fluid can be represented by Eq. (2.67
) and
Eq. (2.48
). The form of
Eq. (2.48
), including only
a Laplacian derivative 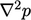 , ensures that
, ensures that 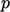 is influenced
instantaneously at all points in the domain by a perturbation in
is influenced
instantaneously at all points in the domain by a perturbation in
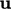 at
any point.
at
any point.
The resulting instantaneous change in
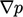 then causes
then causes 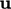 to be redistributed everywhere by Eq. (2.67
), with
further short-range changes due to advection and diffusion
(discussed next).
to be redistributed everywhere by Eq. (2.67
), with
further short-range changes due to advection and diffusion
(discussed next).
The outcome for an incompressible fluid is that
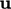 is
influenced instantaneously everywhere in the domain by a
perturbation at any point. In other words, the speed of sound
is
influenced instantaneously everywhere in the domain by a
perturbation at any point. In other words, the speed of sound
 ,
corresponding to propagation of disturbances, is infinite.
,
corresponding to propagation of disturbances, is infinite.
Advection-diffusion equations
Energy conservation can be represented by Eq. (2.65 ), in which perturbations propagate at a characteristic speed due to the advection and diffusion.
Advection propagates at speed  , with a region of
influence
, with a region of
influence 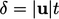 in the direction of flow. The relation can be obtained from
scale similarity when
in the direction of flow. The relation can be obtained from
scale similarity when 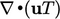 and
and  are similar in magnitude, i.e.
are similar in magnitude, i.e. 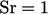 in Eq. (2.69
).
in Eq. (2.69
).
By the same argument, the region of influence for
diffusion coincides with 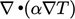 and
and 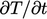 being similar in magnitude, i.e.
being similar in magnitude, i.e. 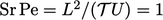 . A diffusion “front”
travels a distance according to
. A diffusion “front”
travels a distance according to  (
( means “of the order of
magnitude”).
means “of the order of
magnitude”).
The diffusion equation, 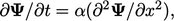 in one dimension
(
in one dimension
(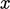 )
has a solution24
)
has a solution24 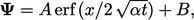 where
where 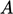 ,
, 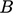 are constants and
are constants and 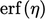 is the error function
below.
is the error function
below.
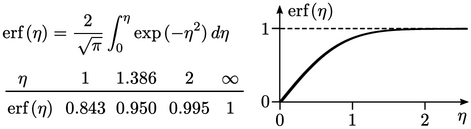
This means that for heat conduction problems,
e.g. in solids, the
distance travelled by the thermal front is 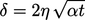 , consistent with
similarity arguments above.
, consistent with
similarity arguments above.
The coefficient 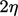 depends on where on the
depends on where on the
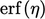 curve the front is located. One option is
curve the front is located. One option is  , where the solution is
within 0.5% of the asymptote of 1.
, where the solution is
within 0.5% of the asymptote of 1.

