Notes on Computational Fluid Dynamics: General Principles

2.10 Fluid deformation

Conservation of momentum Eq. (2.19 ) includes the 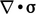term describing the forces within a fluid. At a macroscopic level, the forces exist due to interactions between fluid particles and change due to deformation of the fluid as it moves.

From the velocity field 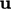, we need to isolate pure deformation of the fluid from other characteristics of the flow. The figure below shows a rectangular fluid element under shear in the 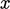-direction due to a uniform velocity gradient in the 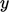-direction.

The velocity gradient 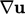calculates some rate of shear of the rectangular element. The upper diagram shows shear in one direction, known as parallel shear.

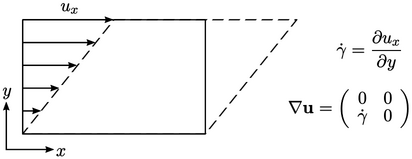
Parallel shear can be decomposed into pure shear (left) and a rotation (right). The rotational component is represented by the skew part of 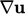, see Eq. (2.25 ). Since a rotation does not involve deformation, it must be removed from any measure of it, which leaves the symmetric part of the tensor.

Therefore, the rate of deformation tensor 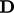and spin (rotational) tensor 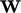are defined as

(2.33)

Trace of a tensor

The trace of a tensor 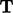is the sum of the diagonal components, producing a scalar

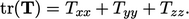(2.34)

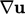Where the tensor is , we conclude from Eq. (2.13 ) that

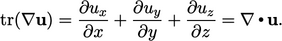(2.35)

Deviatoric and spherical tensors

A tensor can be decomposed into the sum of its deviatoric part and a spherical part as follows:

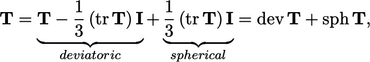(2.36)

where is the identity tensor, see Eq. (2.30 ). The deviatoric part subtracts the mean of the trace from each diagonal component such that the resulting tensor is “trace-free”, i.e. 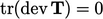.