2.18 Heat capacity
When the heat conduction model of
Eq. (2.54
) is substituted into
Eq. (2.51
), we produce an equation with two
variables 
and 
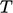. For example, starting with Eq. (2.56
) for internal energy, and
ignoring mechanical power and heat source terms, gives
 |
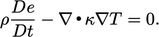(2.60) |
and
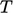is
needed. Heat capacity
provides this, describing an amount of heat required to produce a
unit change in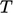 
. We use specific heat capacity, relating to a constant volume process, whose SI
units are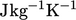 
, defined as
 |
(2.61) |
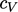.19 It
calculates that any degree of
freedom (DoF), such as a component
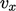of
particle translational velocity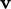 
,
which appears quadratically in
energy, i.e. as
,
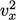contributes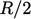 
to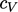 
.
For monatomic gases,
e.g. argon Ar,
particle motion is translational only (until atoms dissociate into
subatomic particles). With 3 translational DoFs,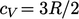 
is constant.
A gas which obeys the ideal gas law with constant
is
known as calorically
perfect.
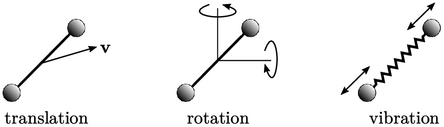
For diatomic gases,
e.g. nitrogen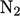 
, molecular
motion is translational (left) and rotational (centre) at lower
temperature (in the gas state). At higher temperature, vibrational
motion is excited along its bond (right). Heat capacity
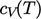for
diatomic gases are then a function of temperature as shown below
for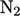 
.
Rotational motion provides 2 DoFs (rotational
energy about the axis is negligible), giving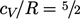 
. Beyond 500K,
vibrational motion provides 2 additional DoFs (one kinetic, one
potential), causing a gradual transition to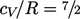 
. At high temperature,
molecules dissociate and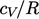 
increases further.
A thermally
perfect gas is
an ideal gas with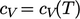 
. Often 
can be treated as constant over a range of
,
e.g. T 
600K for
.
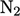Otherwise, accurate calculations require a suitable model of
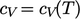. An
imperfect gas exhibits
.
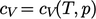