2.9 Conservation and boundedness
The material derivative Eq. (2.14
) includes the
term. However, the term can take for the form 
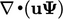, by applying
conservation of mass Eq. (2.8
), as shown in Sec. 2.8
. The two terms are related by
the product rule
 |
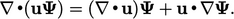(2.31) |
While the two terms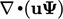 
and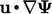 
appear similar,
they affect the solution of an equation is different ways.
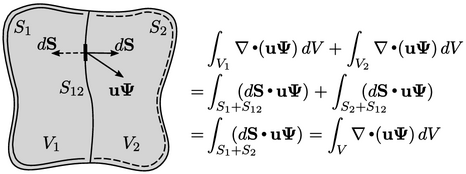
The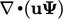 
term maintains conservation in 
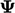. All variables
are inside (to the right of) the divergence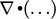 
, so when we integrate
it over a volume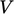 
, it can be entirely transformed by Gauss’s
theorem to an integral of the flux of
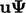at
.
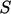If we split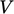 
into two sub-volumes
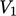and
,
the surface integrals are also split over two surfaces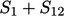 
and
,
where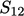 
is the part of the surface common to both volumes.
The fluxes at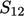 
for each sub-volume
have equal magnitude but opposite sign, since their respective
surface area vectors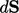 
point outwards from the volume in opposing
directions. These fluxes cancel one another out, such that the sum
of integrals over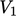 
and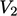 
is identically equal to the integral over
.
Thus, the term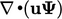 
ensures conservation in
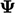across a surface separating regions of the flow domain. Conservation
is guaranteed at all points in the limit 
for any sub-volume.
The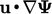 
form cannot transform to a surface integral so
does not ensure conservation. Instead it ensures boundedness, as demonstrated by
the solution of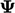 
in the following equation in one (
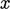) dimension
(1D)
 |
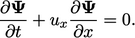(2.32) |
. If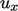 
is uniform, then
the profile of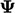 
does not change but simply translates at a speed
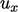as
shown in the left diagram. If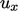 
varies with
,
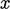the profile changes, e.g. flattens, as shown in the
right diagram.
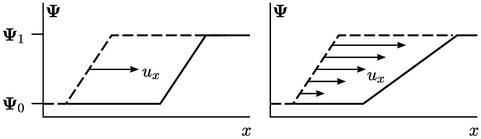
In both cases, the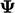 
profile remains within the original bounds of
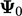and
;
the solution is said to be bounded. While the behaviour is
illustrated in 1D, it extends to 3D.
Thus, the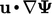 
term ensures boundedness. By contrast, the
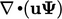term, while ensuring conservation, does not ensure boundedness when
.
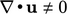The two terms are connected by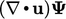 
which changes
due
to expansion/contraction of the fluid, as discussed in
Sec. 2.4
. Its effect is illustrated by
flattening of the profile in the right diagram, since a non-uniform
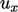corresponds to 
.
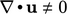