2.6 Forces at a surface
The next law to define is that of conservation
of momentum, i.e. Newton’s
second law of motion (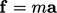 ) for fluids. It involves forces within the fluid
so requires a description of forces at a surface
) for fluids. It involves forces within the fluid
so requires a description of forces at a surface  bounding a volume
bounding a volume
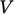 .
.
The force 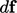 is in the direction of
the traction vector with magnitude of (traction
is in the direction of
the traction vector with magnitude of (traction  surface area) —
compare with Eq. (2.3
)
surface area) —
compare with Eq. (2.3
)
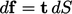 |
(2.16) |
Instead, we require 3 traction vectors  ,
,  and
and 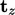 , defined in planes
perpendicular to one another, i.e.
, defined in planes
perpendicular to one another, i.e. 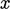 ,
, 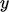 and
and  . This results in
the stress tensor
. This results in
the stress tensor
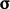 with 9
components, consisting of 3 traction vectors, each containing 3
components.
with 9
components, consisting of 3 traction vectors, each containing 3
components.
The traction can be calculated at a surface with
any orientation by taking the inner product of the unit normal
vector 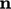 and the stress tensor
and the stress tensor 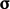 such that
such that
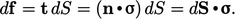 |
(2.17) |
Tensors
We have defined the stress tensor3, an
entity with 9 component values, corresponding to our 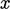 ,
,  and
and
 axes (or more specifically base
vectors of unit length aligned with our
axes (or more specifically base
vectors of unit length aligned with our 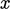 ,
,  and
and  axes).
axes).
In fact, the term “tensor” describes any entity
with multiple component values corresponding to the dimensions of
space — here 3. A tensor has rank  ,
such that the number of component values for 3D space =
,
such that the number of component values for 3D space = 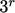 .
.
In this book we use the term “tensor” to mean “tensor of rank 2” unless otherwise noted. A vector is a tensor of rank 1 and a scalar is rank 0.
The inner product of a vector 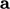 and tensor
and tensor
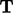 produces a vector whose 3 components are evaluated as follows:
produces a vector whose 3 components are evaluated as follows:
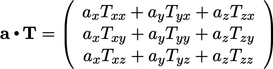 |
(2.18) |
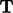 is symmetric since
is symmetric since
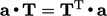 —
see Eq. (2.24
) for the transpose
—
see Eq. (2.24
) for the transpose 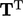 .
.

