Notes on Computational Fluid Dynamics: General Principles

2.1 Pressure

The equations of fluid dynamics in CFD treat the fluid as a continuous medium, or continuum. It is continuous in the sense that we consider the fluid as having no “empty space” by ignoring its molecular nature. We assume it has properties that vary from point to point and are continuous throughout the solution domain, and whose derivatives are also continuous.

Pressure is an important property of a fluid, denoted by 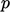. It describes the amount of force per unit surface area which acts on a surface, in the direction perpendicular to the surface.

Pressure is a scalar that produces a force vector with direction normal to the surface. When pressure is applied to one side of a segment of surface with area 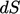, the force 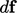points away from that side by

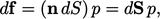(2.3)

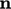where is the vector of unit length, normal to the surface 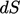. The term vector denotes a geometric entity with magnitude and direction; a surface can be represented by a surface area vector 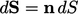of magnitude 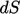and direction .

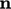While pressure exerts a force on a surface, the fluid experiences a force which is compressive in nature, assuming is positive.

Pressure is measured in SI units of pascal 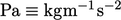. From Sec. 2.13 onwards, however, we generally use 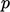to represent the kinematic pressure, in units 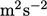, obtained by dividing the true pressure by a constant density .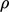

Scalar fields

The majority of properties, e.g. pressure, temperature, energy, density, volume, etc., can be represented by a single number, or scalar. A scalar field describes a scalar property, e.g. pressure, which varies from point to point across some spatial domain.

Point locations can be defined in any co-ordinate system of axes, e.g. Cartesian (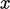, , 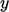), and in any orientation. A scalar field is invariant, meaning the scalar values are the same irrespective of the co-ordinate system used.

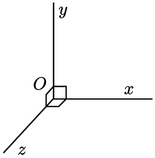
In this book, space and fields will be described in a co-ordinate system with right-handed rectangular Cartesian axes. The axes are constructed by defining an origin 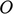from which three lines are drawn at right angles to each other, termed the 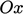, , 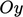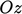axes. A right-handed set of axes requires that looking down the 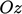axis with 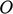nearest, an arc from the 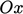axis to the axis is in a clockwise sense.