2.12 Newtonian fluid
In Sec. 2.6 we introduced forces in a fluid. At the macroscopic scale of a continuum, we characterise a fluid’s response to applied forces through constitutive models.
The Newtonian (or linear viscous) fluid is the
most common constitutive model that represents the behaviour of
many liquids and gases. It states that a fluid at rest (or uniform
velocity) does not sustain shear stress 
; it can be expressed
by
 |
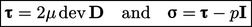(2.41) |
The model is a continuum
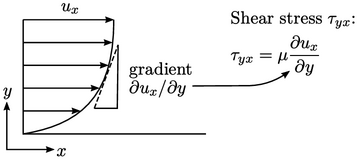
representation9 of Newton’s law of viscosity10
which states that shear stress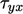 
is proportional to
velocity gradient by the dynamic viscosity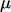 
.
It is a specific case of the more general
Stokesian fluid,
defined as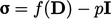 
, where 
is deformation rate, Eq. (2.33
). The Newtonian model
assumes: (1) the fluid is isotropic,
i.e. the value of
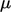is
independent of the direction in which it is measured; (2) zero
bulk viscosity associated with a change
in volume o the fluid.
Using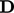 
in Eq. (2.41
) ensures that the shear stress
is induced by deformation only. Taking the deviatoric part,
,
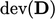ensures viscous stresses are not generated by volume changes, which
are represented by 
.
This is due to the “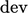
” operator subtracting
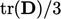from each diagonal
component of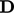 
, giving a total of 
(
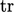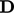) from all 3 diagonal
components. From Eq. (2.35
), 
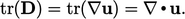
Pressure gradient
When we substitute Eq. (2.41) in
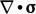in
Eq. (2.19
), the pressure part is
.
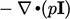The term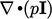 
is equivalent to gradient 
.
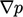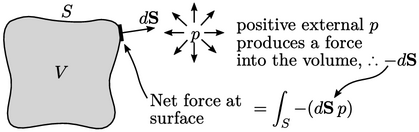
Like divergence of stress in Eq. (2.22
), the gradient of
pressure represents the pressure flux across the surface per unit
volume as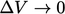 
, according to
 |
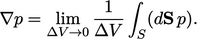(2.42) |
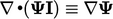holds for any variable 
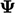, a gradient term is
conservative, like divergence, and can be converted to a surface
integral under an equivalent Gauss’s Theorem
 |
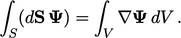(2.43) |
