2.3 Flow through a surface
The concept of flow through a surface appears in many areas of CFD, including fluid dynamics equations, numerical methods, boundary conditions and general flow calculations. When we talk about something that travels through a surface, the term flux is generally used.2
To quantify the flux of some property, we multiply
the area of surface by the property at the surface. If the property
is a vector, we take the component normal to the surface. For example, the
flux 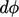 associated with velocity through a surface segment of area
associated with velocity through a surface segment of area
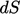 would be
would be  .
.
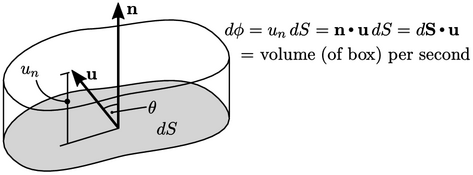
As shown in the figure,  can be calculated from
can be calculated from
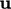 by
the inner product with normal vector
by
the inner product with normal vector 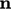 of unit length, expressed as
of unit length, expressed as
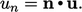 |
(2.5) |
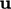 is
is
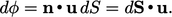 |
(2.6) |
 first since the order matters with a tensor,
e.g. stress
first since the order matters with a tensor,
e.g. stress 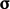 , introduced in
Sec. 2.6
, i.e.
, introduced in
Sec. 2.6
, i.e. 
Inner product of two vectors
The normal component of velocity 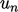 is described in
Eq. (2.5
) by the inner, or “dot”, product
of
is described in
Eq. (2.5
) by the inner, or “dot”, product
of 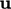 and
and 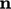 . It is calculated for vectors
. It is calculated for vectors 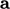 and
and 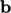 as shown in the
figure below, where
as shown in the
figure below, where  denotes the magnitude of the vector and
denotes the magnitude of the vector and
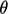 is
the internal angle between the two vectors.
is
the internal angle between the two vectors.
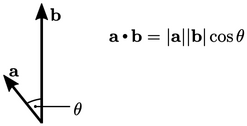
The inner product of two vectors is a scalar invariant, since the magnitudes and angle are the same irrespective of the co-ordinate system used. It is calculated from vector components as follows:
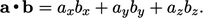 |
The inner product of two vectors is commutative,
i.e. 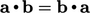 . It is distributive,
i.e. with an additional
vector
. It is distributive,
i.e. with an additional
vector  ,
,
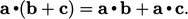 |
Scalar multiplication and inner products are associative, i.e.
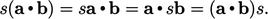 |
An inner product of a vector with itself is simply the square of the vector magnitude, i.e.
 |
(2.7) |

