Notes on Computational Fluid Dynamics: General Principles

Chapter 3 Numerical Method

Chapter 2 described:

• the main governing equations of fluid dynamics, namely conservation laws of mass, momentum and energy;
• standard models for diffusion of momentum and heat, namely Newton’s law of viscosity and Fourier’s law of conduction;
• the ideal gas equation of state and specific heat capacity;
• tensor algebra used in the equations and the derivatives of time, divergence, gradient and Laplacian.

Sets of governing equations and models are combined to simulate different flow problems. Numerical methods are used in CFD to solve the equations since closed-form, analytical solutions only exist for very simple geometries and flow regimes.

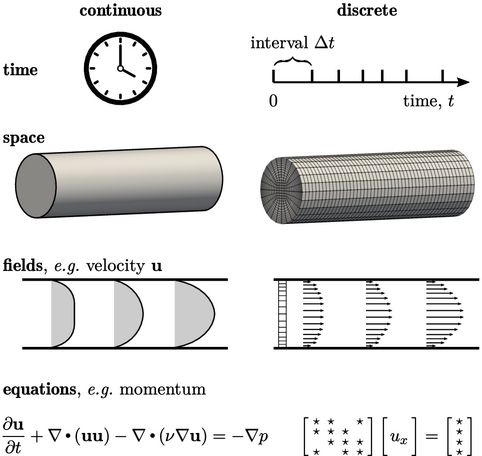
The numerical methods represent continuous physical entities by equivalent discrete entities, i.e.:

• time is split into intervals of duration ;
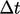• space becomes cells of a mesh — the solution domain;
• fields, e.g. 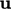, become discrete values, e.g. one per cell;
• partial differential equations, e.g. for momentum, become a set of linear equations.

There are numerous discretisation methods to create the set of linear equations, but this book specifically examines the finite volume method.

The sets of equations can be solved using a variety of algorithms, with finite volume discretisation lending itself towards iterative methods.