3.8 Surface normal gradient
The surface normal gradient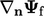 
is a part of the
Laplacian discretisation Eq. (3.2
), illustrated in
the figure below.
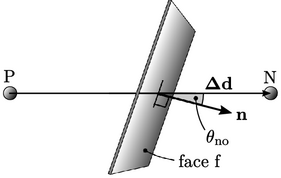
The discretisation of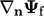 
is built upon a finite
difference of cell values on each side of the face according
to
 |
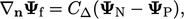(3.5) |
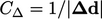. When this orthogonal scheme
is applied to Eq. (3.2
) to discretise a
Laplacian, it forms coefficients 
of a matrix equation
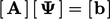since it references cell values of the field 
. For cell 
, the coefficient
for each neighbour cell (
) is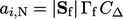 
and the diagonal
coefficient is the negative of the sum of neighbour coefficients:
.
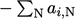Discretisation of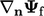 
by Eq. (3.5) is most
accurate when the face is orthogonal to
,
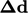i.e. the angle 
between
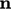and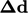 
is zero. However, if the face is non-orthogonal,
the error associated with Eq. (3.5
) increases with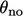 
.
Non-orthogonal correction
A more accurate discretisation of 
at a
non-orthogonal face is formed of the vector sum of the orthogonal
scheme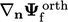 
and an explicit
correction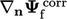 
. The latter is calculated from the full gradient
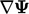in
adjacent cells (described in Sec. 3.15
), interpolated to the face
.
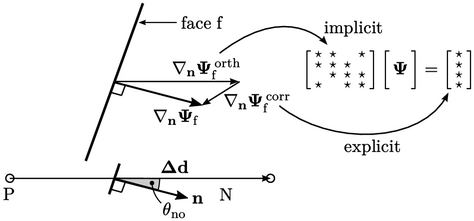
The correction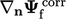 
is explicit, i.e.
calculated using known values of 
, so may need updating
within an iterative sequence to maintain accuracy, as discussed in
Sec. 5.20
. To ensure that the
iterative sequence converges, the implicit contribution is elevated by replacing 
in the orthogonal
scheme with
 |
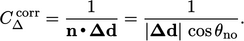(3.6) |
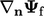scheme combines the implicit and explicit parts by
 |
(3.7) |
. For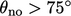 
, stability can be
maintained at the expense of accuracy by limiting the magnitude of the
correction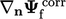 
below some fraction of the magnitude of the
orthogonal 
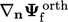part.
