3.1 The finite volume concept
There are many numerical methods which can be used to solve the partial differential equations encountered in fluid dynamics. No single method is unequivocally better than others. Rather, the efficacy of each method depends on aspects of the case being simulated, e.g. its size, the required level of accuracy and the characteristics and complexity of the equations being solved.
For a method to be useful, it needs to be programmed into software. Complex programs require good design and design relies on good concepts. So inevitably the concepts behind any method are as important as the details contained within.
The finite volume method adopts the idea of control volumes used to create models of physical systems. A control volume represents a region of space, which is generally fixed, enclosed by a surface through which fluid flows in and out.
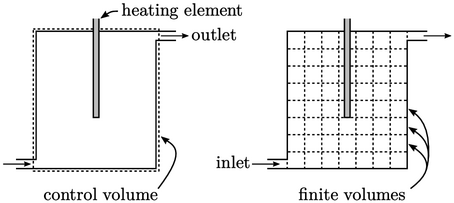
It applies conservation equations, e.g. of mass, momentum and energy, by balancing fluxes, due to inflow and outflow at the bounding surface, with additional sources within the volume. Rather than using a single control volume to describe an entire physical system, e.g. a heating tank, the finite volume method splits the system domain, i.e. the tank, into multiple connected finite volumes. Conservation equations are applied to each volume, ensuring that the fluxes of mass, momentum and heat across surfaces are consistent between the volumes they connect.
The perceived wisdom is that the finite volume method was first introduced in the early 1970’s. But the PhD thesis of Runchal1 from 1969 describes a method which is clearly finite volume. He also published the figure reproduced below,2 which displays the computational mesh as a set of connected control volumes.

Runchal credits the idea to his PhD supervisor Brian Spalding who provided an analogy of tanks connected by tubes in 1967. It captures the essence of finite volume, which uses a mesh to define a physical system of control volumes. Its emphasis is on calculating fluxes between volumes and ensuring conservation.
By contrast, other methods, e.g. finite element, use the mesh to construct mathematical functions to calculate distributions of properties. The finite volume method does not do that.

