3.16 Gradient limiting
The standard gradient calculation can generate values with an unphysically large magnitude when cell quality is poor. A large gradient value in one cell can contribute sufficiently to the source term of an equation to cause unboundedness in the solution.
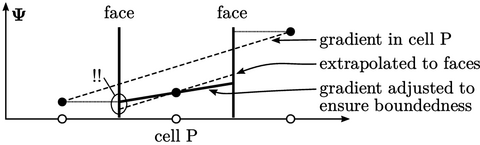
The calculated gradient can be limited to avoid unphysical values. The
limiting extrapolates the cell values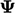 
using the gradient to
all neighbouring face
centres. If the extrapolated 
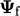at a face
falls outside of the bounds of 
at neighbouring cell
centres, the gradient is adjusted to match the bounding value.
This numerical scheme has an advantage that is takes into account all surrounding cells so is fully “multi-dimensional”. It ensures boundedness locally between cells so can help eliminate instabilities in advection discretisation.
Linear upwind with gradient limiting
Limiting can be applied to the cell gradient in the explicit contribution of the linear upwind advection scheme, described in Sec. 3.14 . The scheme with gradient limiting is analysed below for its TVD behaviour on a regular mesh in 1D.
In the following figure, the cell gradient is
denoted by “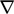
” and the face gradient is denoted by “
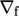”. The ratio of
gradients is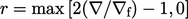 
from Eq. (3.12
), which is adjusted by modifying
.
No limiting is applied for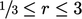 
, when 
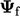can be expressed by
with 
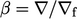. In that case, 
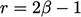, corresponding to a function 
.
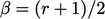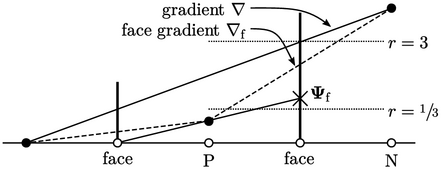
Limiting is applied for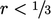 
, reducing the gradient
linearly to zero as 
. This corresponds to a function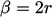 
for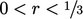 
. Similarly,
limiting is applied when 
. Within that range, 
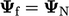so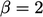 
.
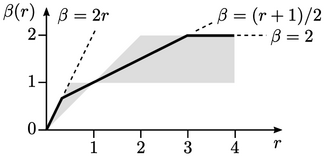
On a Sweby diagram linear upwind with gradient
limiting is TVD, with the line 
being the regime with
no gradient limiting.
This function uses too much downwind interpolation to be a reliable TVD scheme for advection. However, as a gradient limiter for the linear upwind scheme, it is strongly bounded, due to the multi-dimensional nature of gradient limiting — with good accuracy due to the skewness correction in linear upwind.
