Notes on Computational Fluid Dynamics: General Principles

3.11 Limited advection schemes

Alternative schemes for advection attempt to overcome problems with boundedness and accuracy of the linear and upwind schemes respectively. Many schemes apply a limiter 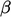between 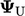from upwind and 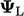from the linear scheme Eq. (3.4 ) according to

(3.11)

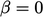When , the scheme reduces to upwind and it becomes linear interpolation when 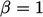. For a uniform mesh (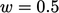), represents interpolation using the downwind cell value.

Limited schemes attempt to optimise at each face, based on the local 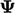, to maximise accuracy whilst maintaining boundedness.

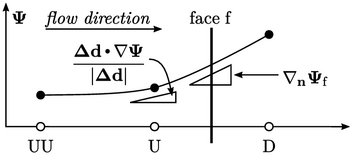
Many schemes analyse the change in gradient of 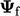between the face and upwind cell in the direction connecting cell centres. They define a function of a ratio of consecutive gradients as:

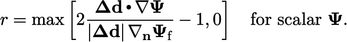(3.12)

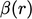There are numerous published schemes that define the limiter as a function of the gradient ratio . Those schemes that are most useful are described in the following sections.

Total variation diminishing schemes

Many useful schemes fall into a class known as Total Variation Diminishing (TVD).⁷ The TVD idea is that if the total variation of field 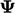does not increase in time, “overshoots” and oscillations associated with unboundedness will not occur.

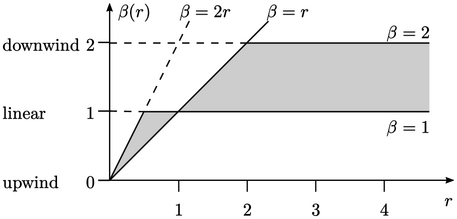
To qualify as TVD, the limiter function 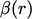must fall within the shaded area in a Sweby diagram (above).⁸ The TVD concept is a 1D analysis. For 3D CFD on irregular polyhedral meshes, oscillations are more likely to occur with TVD schemes whose 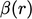functions tend significantly to downwind, i.e. towards the upper part of the shaded area near .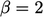

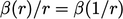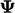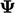A further property of a limited scheme is symmetry. A scheme is symmetric when the condition is satisfied. When this occurs, the scheme applies the same limiter to the gradient of , irrespective of the sign of its gradient. As a consequence, a property , initialised with a symmetric profile, e.g. a bell curve, will retain its symmetry under advection.

---

---