3.19 Calculated derivatives
The introduction to matrix construction,
Sec. 3.5
, described implicit
and explicit discretisation of terms in an equation. It concluded
that the principal derivatives of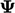 
that can be treated
implicitly — forming matrix coefficients in 
— are a time
derivative, advection and Laplacian.
Terms with other derivatives must be calculated
from respective fields, e.g.
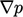from current values of 
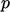. In Sec. 3.15
, we have described
discretisation of a gradient, which is always explicit. This
section gathers together the other derivatives found in equations
for fluid dynamics and associated models.
General divergence term
A general divergence term is any term that can
be represented by 
. It excludes the Laplacian term which includes
a gradient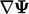 
, and advection which includes 
.
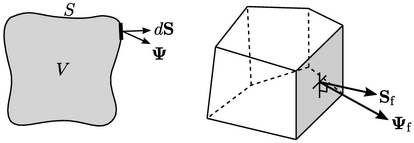
The discretisation of a general divergence term
is an explicit calculation using current values of 
. It is based on a
surface integral using the divergence definition in
Sec. 2.23
as shown below:
 |
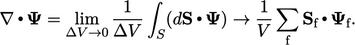(3.30) |
is generally interpolated from cell values using the
linear scheme. Terms discretised using this scheme include
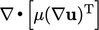in
Eq. (2.45
), a divergence of
stress 
, etc.
Curl of a vector
The curl derivative 
is calculated from the
gradient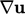 
and applying the Hodge dual operator given by
Eq. (2.40
) using the following
relation:
 |
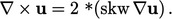(3.31) |
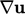is discretised according to a scheme from
Sec. 3.15
, from which 
is calculated by
Eq. (3.31
).
Mag-square grad-grad
A derivative which appears in some model
equations is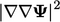 
, described as “mag-square grad-grad”. This derivative
returns a scalar since the mag-square, e.g.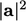 
, represents the inner
product of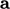 
with itself, as shown in Eq. (2.7
).
The mag-square calculation always uses the
appropriate inner product to reduce the result to a scalar. For a
tensor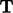 
, it is the double inner product, i.e. 
.
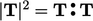The grad-grad operator 
yields a third-rank
tensor in the case that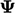 
is a vector field. To avoid storing
third-rank tensors, the mag-square grad-grad operator is evaluated
by summing the result from the operator on each component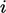 
of 
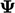by
 |
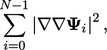(3.32) |
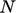is the number of components in 
.
