3.10 Upwind scheme
The upwind scheme represents the face value
 by
the value
by
the value  in the cell upwind of the face. The advantage of upwind is
that it can guarantee
boundedness of a field
in the cell upwind of the face. The advantage of upwind is
that it can guarantee
boundedness of a field  . We can demonstrate
this point by revisiting the 1D
Eq. (2.32
) in Sec. 2.9
:
. We can demonstrate
this point by revisiting the 1D
Eq. (2.32
) in Sec. 2.9
:
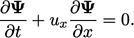 |
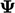 by
equating changes in
by
equating changes in 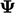 in time to the local gradient
in time to the local gradient 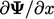 . If we apply
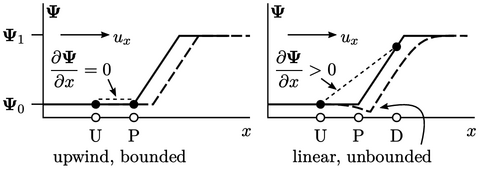
upwind to calculate the change at point P, the gradient
. If we apply
upwind to calculate the change at point P, the gradient
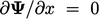 and no change in
and no change in  is correctly calculated (left).
is correctly calculated (left).
However, linear differencing between upwind and
downwind values results in 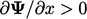 , so predicts a decrease in the value at P
(right). The solution produces a solution with
, so predicts a decrease in the value at P
(right). The solution produces a solution with 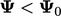 , so is unbounded.
, so is unbounded.
Boundedness of the conservative form of advection
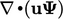 is
only guaranteed when
is
only guaranteed when 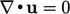 , as discussed in Sec. 2.9
. In 1D, the conservative form
moves
, as discussed in Sec. 2.9
. In 1D, the conservative form
moves  inside the derivative
inside the derivative 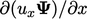 . That gradient is only
zero with upwind when
. That gradient is only
zero with upwind when 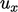 is uniform, i.e. the 1D equivalent to
is uniform, i.e. the 1D equivalent to 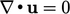 .
.
Diffusion of upwind
The upwind scheme is highly diffusive which can result in poor accuracy. Its diffusive nature can be explained by considering the following Taylor’s series expansion:
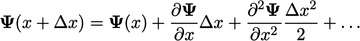 |
(3.9) |
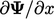 using
using 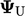 and
and
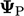 at
locations U and P, separated by distance
at
locations U and P, separated by distance  . Relating the upwind
calculation to Eq. (3.9
) gives
. Relating the upwind
calculation to Eq. (3.9
) gives
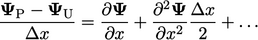 |
(3.10) |
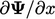 but also the
second derivative
but also the
second derivative 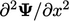 (and higher derivatives).
(and higher derivatives). 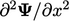 is equivalent to a
Laplacian, described in Sec. 2.14
, which diffuses
is equivalent to a
Laplacian, described in Sec. 2.14
, which diffuses 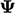 with a
diffusivity proportional to
with a
diffusivity proportional to 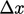 .
.

The upwind scheme is particularly diffusive when
the flow direction is not aligned with the cells of a mesh. In the
2D box of cells above, 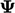 is advected at a
is advected at a 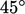 angle, beginning with
an abrupt step change from
angle, beginning with
an abrupt step change from 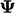 = 1 and
= 1 and 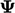 = 0 between
the left and lower boundaries. The step rapidly diffuses along the
direction of travel as shown in graph (right) and shaded area
(left).
= 0 between
the left and lower boundaries. The step rapidly diffuses along the
direction of travel as shown in graph (right) and shaded area
(left).

