3.21 Terms which change sign
An equation may include a function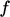 
which can
return a value which is positive or negative, e.g.
 |
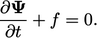(3.37) |
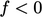and ensure the solution exceeds the lower bound
of 0 when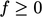 
. The discretisation of 
is therefore treated
implicitly or explicitly within each cell based on
 |
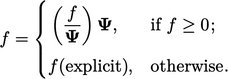(3.38) |
Maintaining lower and upper bounds
The solution variable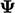 
could have a physical
bound at any low value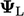 
and/or high value 
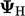. We can treat the
function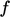 
in Eq. (3.37
) as follows to
maintain boundedness:
 |
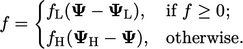(3.39) |
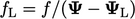and 
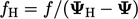are calculated using the current values of
.
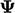If we examine the situation with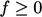 
,
Eq. (3.37
) would be
discretised as
 |
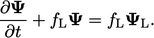(3.40) |
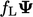implicitly alongside the Euler time scheme,
Eq. (3.40
) becomes:
 |
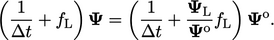(3.41) |
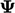decreases when 
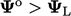, but cannot fall below
the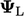 
bound within a solution step. In the limit that
,
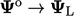the solution for 
no longer decreases.
An equivalent analysis shows Eq. (3.40
) maintains
boundedness for the upper bound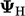 
. In that case, note
that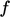 
is negative so the term in 
can still be treated
implicitly.
Fields bounded by 0 and 1
Many properties are expressed as a fraction, e.g. concentration of a chemical species, so are bounded by 0 and 1. When that happens, Eq. (3.39 ) simplifies to
 |
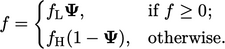(3.42) |
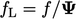and 
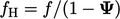are calculated using the current values of
.
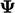It is particularly important to maintain
boundedness of a field with 0-1 bounds when it is used to calculate
another property which has a physical bound. For example, in a
system of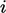 
fluid phases, fluid 
can be calculated by 
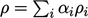from phase fractions
and densities 
.
A small amount of unboundedness in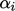 
, in the phase
with highest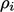 
, causes large unboundedness in 
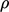, e.g. in 2 phases with 
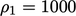and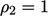 
, the
calculated 
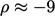with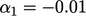 
.
