3.14 Linear upwind scheme
Linear
upwind is another significant scheme for advection. It is
used particularly for advection of momentum, i.e.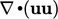 
or 
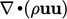but can be
effective for advection of other variables.
The scheme reduces the diffusive nature of
upwind by including additional upwind cell values indirectly from
the gradient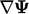 
in the upwind cell.
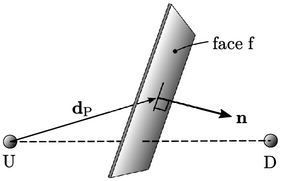
Linear upwind describes the face value as an
extrapolation of the upwind cell value to the face using the upwind
cell gradient 
and a vector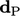 
from the cell centre to face centre. It
first provides a contribution to the coefficients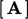 
of a matrix equation
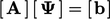by
representing face values 
by the upwind value 
. The extrapolation is
then introduced through an additional explicit contribution 
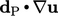to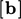 
.
Skewness
Interpolation of values between cell centres is along a line joining the cell centres. Any interpolated value at a face relates to the point on the face intersected by that line.
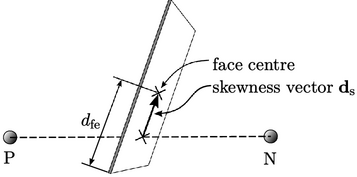
Skewness is the distance between the
intersection point and the face centre. It can be represented by a
vector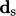 
or as the ratio 
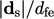, where 
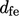is the distance from
the face centre to edge in the direction of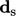 
.
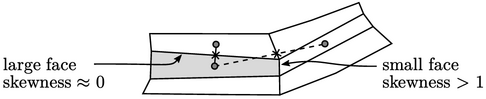
An interpolated value represents an average
across a face, but as skewness increases, this representation
becomes less accurate. High skewness (e.g. 
1) does not
immediately equate to poor accuracy, however, since interpolated
values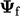 
are multiplied by face areas within a surface integral,
e.g. 
— and high skewness
occurs at small faces.
Advection schemes do not generally include a
correction for high skewness to improve accuracy. However, the
linear upwind scheme naturally includes skewness correction since
the explicit contribution is in the direction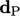 
towards the face
centre.
