3.6 Overview of discretisation
The choice of numerical method determines how
coefficients for 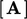 and
and 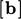 are calculated and consequently the
characteristics of the resulting matrix equation
are calculated and consequently the
characteristics of the resulting matrix equation 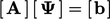 .
.
The finite volume method described here is firmly rooted in the underlying concept of control volumes, described in Sec. 3.1 . It uses integrals over a surface surrounding a volume applied to irregular polyhedral meshes, described in Sec. 3.2 .
The discretisation is described in terms of
differential operators, e.g.
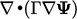 and
and 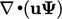 , applied to a general field
, applied to a general field 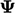 .4
.4
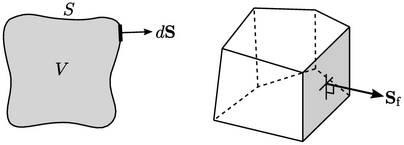
The main concept is that faces within a mesh form
closed surfaces surrounding finite volumes, e.g. a single cell. Any surface
integral that represents a derivative, e.g.  , is approximated by a
summation over the faces ‘
, is approximated by a
summation over the faces ‘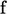 ’ that form the surface, i.e.
’ that form the surface, i.e.
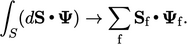 |
 , i.e.
, i.e.  , must then be
calculated. The value
, must then be
calculated. The value  is required at each face, which must be calculated by some
method of interpolation of values of
is required at each face, which must be calculated by some
method of interpolation of values of
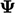 from cells neighbouring the respective face.
from cells neighbouring the respective face.
Intensive and extensive properties
In this chapter, derivatives and their
discretisation are described at a
point, e.g.
 ,
e.g. Eq. (3.8
):
,
e.g. Eq. (3.8
):
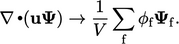 |
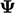 simply produces another field (with values defined at cell centres,
with units of
simply produces another field (with values defined at cell centres,
with units of 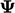 /time).
/time).
The resulting field is 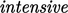 , meaning it is
independent of the size of the system/geometry. Like other
intensive fields, e.g.
, meaning it is
independent of the size of the system/geometry. Like other
intensive fields, e.g.
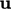 and
and 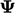 themselves, it can be used in further calculations,
e.g. within another
derivative or added/subtracted from other fields.
themselves, it can be used in further calculations,
e.g. within another
derivative or added/subtracted from other fields.
Extensive
properties are dependent on the size of the system. For example,
the volumetric flux 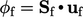 described in Sec. 3.9
is dependent on
the face areas
described in Sec. 3.9
is dependent on
the face areas 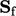 . Numerical operations involving extensive properties,
e.g. addition, subtraction,
or mapping to another location, generally produce meaningless data.
. Numerical operations involving extensive properties,
e.g. addition, subtraction,
or mapping to another location, generally produce meaningless data.
While calculations of derivatives yield
intensive fields, matrix equations
are constructed in extensive form, with coefficients and
source vector scaled by cell volume 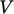 . In other words, in
the discretisation example above, the multiplication by
. In other words, in
the discretisation example above, the multiplication by
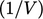 would be omitted.
would be omitted.
There is no 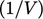 multiplier in the
discretisation of terms which do not involve a surface integral,
e.g. time derivative
Eq. (3.21
) and terms in
Sec. 3.20
. For those terms, the
calculation of matrix coefficients and sources includes a
multiplication by
multiplier in the
discretisation of terms which do not involve a surface integral,
e.g. time derivative
Eq. (3.21
) and terms in
Sec. 3.20
. For those terms, the
calculation of matrix coefficients and sources includes a
multiplication by 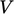 .
.

