3.17 Time discretisation
A local time derivative  in an equation can be
discretised as a finite difference in time. Time
in an equation can be
discretised as a finite difference in time. Time  is expressed in
discrete intervals, or steps, of duration
is expressed in
discrete intervals, or steps, of duration 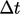 .
.
The Euler
scheme calculates
the derivative from the field at the current time 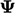 and the previous,
or old, time level
and the previous,
or old, time level
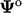 by:
by:
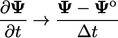 |
(3.21) |
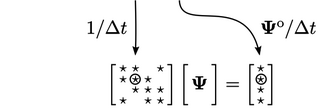
 and to the source vector
and to the source vector 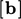 .
.
Courant number
For a 1D domain in the  -direction, the Courant
number is the following dimensionless parameter for each cell of
length
-direction, the Courant
number is the following dimensionless parameter for each cell of
length  :
:
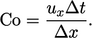 |
(3.22) |
 across all cells.
across all cells. 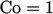 corresponds to a fluid
particle moving across one cell in one time step, so its relevance
to solution convergence is perhaps unsurprising.
corresponds to a fluid
particle moving across one cell in one time step, so its relevance
to solution convergence is perhaps unsurprising.
In an explicit
solution, the convergence limit can reduce further to 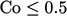 or
or
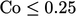 ,
with more accurate schemes for advection. But the finite volume
method is generally implicit so
stability can then be maintained with a higher maximum value of
,
with more accurate schemes for advection. But the finite volume
method is generally implicit so
stability can then be maintained with a higher maximum value of
 .
Temporal accuracy is then the important consideration when choosing
the
.
Temporal accuracy is then the important consideration when choosing
the  of a simulation, both in terms of its mean and maximum
value across all cells in the domain.
of a simulation, both in terms of its mean and maximum
value across all cells in the domain.
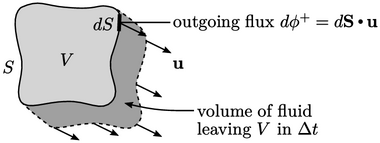
It is therefore important to monitor Courant number which needs to be calculated for 3D problems. Explicit, Euler, upwind discretisation of advection can be presented in 3D as follows:
 |
(3.23) |
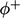 are positive fluxes which transports
are positive fluxes which transports  out of the cell of
interest and
out of the cell of
interest and 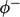 are negative fluxes which transports
are negative fluxes which transports 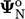 from neighbouring
cells. Since the CFL condition,
from neighbouring
cells. Since the CFL condition, 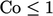 , requires that the
coefficient of
, requires that the
coefficient of  cannot be negative, it follows that
cannot be negative, it follows that
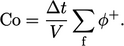 |
(3.24) |
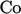 represents the volume of fluid leaving the cell in one time
step, as a fraction of the cell volume, as shown above.
represents the volume of fluid leaving the cell in one time
step, as a fraction of the cell volume, as shown above.

