CFD Direct

The Architects of OpenFOAM

Notes on Computational Fluid Dynamics: General Principles

[chapter contents][previous topic][next topic][index]

5.23 Summary of algorithms and solvers

  • The finite volume method produces sparse matrices, Sec. 5.1 .
  • Symmetric matrices have the same coefficients across the diagonal and advection generally produces an asymmetric matrix.
  • The matrix equations are solved using iterative methods that reduce a residual to a specified tolerance, Sec. 5.4 .
  • Diagonal dominance is a sufficient condition for convergence, see Eq. (5.9 ) and Sec. 5.5 .
  • Under-relaxation may be required to maintain diagonal dominance, Sec. 5.6 , in particular for steady-state solutions.

Gauss-Seidel method

  • Simple iterative method for solutions with cost 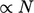eqn, Sec. 5.2 .
  • Effective when the range of influence is short, i.e. 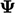eqn in each cell is influenced by changes in close neighbouring cells.
  • The symmetric variant and mesh renumbering may improve convergence, Sec. 5.8 .

Conjugate gradient method

  • A “descent” method which solves a minimisation problem for cases with a longer range of influence, Sec. 5.14 .
  • Solved iteratively, which requires preconditioning to make it efficient, Sec. 5.16 .
  • Symmetric matrix: PCG with DIC preconditioning.
  • Asymmetric matrix: PBiCGStab with DILU preconditioning.

Geometric-algebraic multi-grid (GAMG)

  • Well suited to equations with a long range of influence, in particular the pressure equation, Sec. 5.17 .
  • Simple algebraic agglomeration is corrected by a scaling based on minimisation for Laplacian-dominated equations, Sec. 5.18 .

Systems of equations

  • Systems of equations are solved iteratively with solutions from one equation substituted into the next, Sec. 5.9 .
  • Mass and momentum conservation are coupled by a pressure equation and momentum and flux correctors, Sec. 5.10 .

Steady-state solution

  • Steady flow solutions use the SIMPLE algorithm, Sec. 5.12 .
  • Equations are solved in an iterative sequence with under-relaxation required to ensure convergence, Sec. 5.13.

Transient solution

  • Transient solutions use a PISO loop, Sec. 5.19 .
  • Correction for non-orthogonality in the pressure equation may require a distinct corrector loop, Sec. 5.20 .
  • In the PISO loop, typical configurations solve: 2 pressure equations, each including 1 non-orthogonal corrector; or 3 pressure equations without any non-orthogonal correctors.
  • The PIMPLE algorithm provides additional controls for transient and pseudo-transient simulations, Sec. 5.21 .
Notes on CFD: General Principles - 5.23 Summary of algorithms and solvers