5.18 GAMG method
GAMG is an effective form of multi-grid method used in finite volume CFD. It combines:
- geometric (“G”) agglomeration to define the structure of the coarse meshes;
- the algebraic multi-grid (AMG) method,
where the matrix
is constructed at a coarser level from coefficients at
the finer level, rather than by geometric data from the coarse
mesh.
Agglomeration
Pairwise agglomeration forms coarser meshes by joining pairs of cells at each level of coarsening. In a sweep through the cells, an unpaired cell is paired with the (unpaired) neighbour that shares the face with largest area. This method generally maintains a low aspect ratio (see Sec. 8.2 ) in the resulting agglomerated cells.
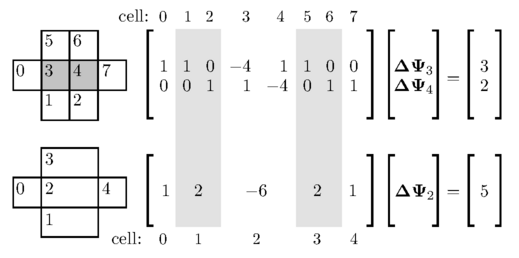
on a 2D mesh of square cells with 
, then
Eq. (3.2
) and
Eq. (3.5
) calculate diagonal
coefficients 
and non-zero off-diagonal coefficients 
.
Algebraic
multi-grid
creates coefficients in the coarser mesh by summing coefficients
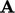and source 
from the finer mesh. The example produces one row of
which is 
.
If the Laplacian for the coarse mesh were
discretised directly, the coefficients in that row would be
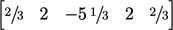due to increasing 
. This discrepancy between agglomerated and
calculated coefficients is repeated in subsequent agglomerations.
Multi-grid begins solving/smoothing for
(with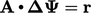 
) at the coarsest mesh. Coarse cell values of 
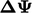are then
injected into corresponding cells in the next finest mesh.
With a Laplacian term, the coefficient discrepancy
caused by algebraic agglomeration causes 
to be under-predicted.
A correction to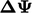 
can be applied by scaling it by a factor
 |
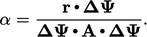(5.37) |
Equation 5.37
is derived by
minimising the error with respect to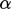 
in the equation
.
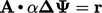The minimisation is performed by setting 
for the quadratic
form
 |
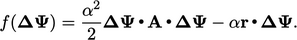(5.38) |
