5.14 Descent methods
The Gauss-Seidel method, introduced in Sec. 5.2 , provides convergent solutions for many problems in CFD. It is most effective when a modest reduction in residual is required, e.g. as part of a steady-state solution described in Sec. 5.12 .
When the Gauss-Seidel method requires a lot of sweeps (e.g. over 10) to converge to a suitable tolerance, alternative methods may be more efficient. Descent methods provide alternative matrix solvers that are often used in CFD.
Descent methods represent the equations which are
being solved as a minimisation problem. It is demonstrated below using a matrix
equation of the form 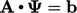 with 2 values
with 2 values
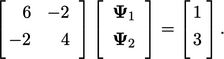 |
(5.27) |
 |
(5.28) |
 |
(5.29) |
 is:
is:
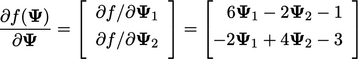 |
(5.30) |
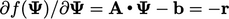 , i.e. the
negative of the residual vector Eq. (5.10
), as verified by the model
example.
, i.e. the
negative of the residual vector Eq. (5.10
), as verified by the model
example.
Equating the gradient to zero, 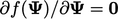 , corresponds to a
minimum in the quadratic function. At the same
time, it is the solution to
, corresponds to a
minimum in the quadratic function. At the same
time, it is the solution to
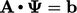 .
The method is therefore concerned with finding the minimum of the
quadratic form efficiently.
.
The method is therefore concerned with finding the minimum of the
quadratic form efficiently.
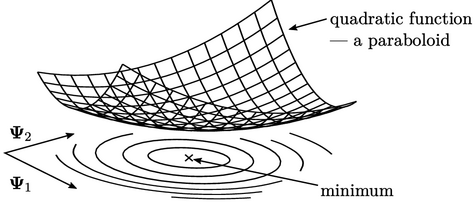
For this method to work, the quadratic form
must have a minimum, which requires that 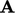 is symmetric and positive-definite. A positive-definite
matrix is hard to
visualise, but for a 2-value function it ensures the quadratic
function is a paraboloid.
is symmetric and positive-definite. A positive-definite
matrix is hard to
visualise, but for a 2-value function it ensures the quadratic
function is a paraboloid.
Diagonal dominance is the convergence condition for the Gauss-Seidel method, discussed in Sec. 5.3 . Importantly, a symmetric matrix that is diagonally dominant, and has positive diagonal coefficients, is also positive-definite.
Matrix operations
The ‘ ’ operation between two single-column
matrices, e.g.
’ operation between two single-column
matrices, e.g.  , in
Eq. (5.28
) is represented in other
texts using matrix notation by a transpose
, in
Eq. (5.28
) is represented in other
texts using matrix notation by a transpose  . For the example in
Eq. (5.27
), it is:
. For the example in
Eq. (5.27
), it is:
![2 3 T h i 1 b = [b ] [ ] = 1 3 4 2 5 = 1 + 3 2 \relax \special {t4ht=](img/index2349x.png) |
(5.31) |

