5.3 Convergence
The Gauss-Seidel method was demonstrated in Sec. 5.2 using a sample problem, Eq. (5.2 ), that converged to within 0.2% accuracy in 9 solution sweeps. This section discusses the criteria for convergence of a solution.
The easiest explanation of convergence considers
the error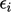 
for each equation 
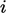, defined in Sec. 5.2
. Substituting 
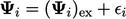in each term
in Eq. (5.3
), e.g. in Eq. (5.3a
), gives
 |
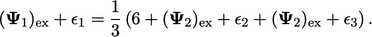(5.5) |
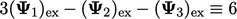, Eq. (5.5
) reduces to
 |
(5.6) |
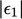is at
least as large as the sum of the terms on the r.h.s., but is
smaller if the signs of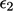 
and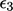 
are different,
i.e.
 |
(5.7) |
The solution begins with an initial error of
,
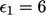and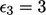 
. After one sweep the error is 
, 
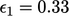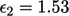and 
.
The error is quickly distributed evenly, such
that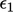 
and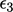 
are almost identical at sweep 2. The errors continue
to reduce since Eq. (5.7
) and
Eq. (5.8
) guarantee that
no error is greater than the average of the other errors.
Condition for convergence
The behaviour of this problem indicates a convergence condition for the Gauss-Seidel method: the magnitude of the diagonal coefficient in each matrix row must be greater than or equal to the sum of the magnitudes of the other coefficients in the row; in one row at least, the “greater than” condition must hold.
This is known as diagonal dominance, which is a sufficient condition for convergence, described mathematically as
 |
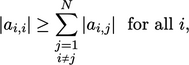(5.9) |
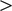’ condition must be satisfied for at least one
.
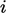The description of the condition as “sufficient” means that
convergence may occur when the condition is not met.
