5.20 Transient solution controls
The following additional controls are commonly used for the transient solution described in Sec. 5.19 :
- an iterative loop around the pressure equation to update any non-orthogonal correction;
- an on/off switch for the momentum predictor.
Non-orthogonal corrector loop
The algorithm solves the pressure equation,
Eq. (5.19
), which
includes the discretisation of the Laplacian term 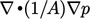 , according to
Sec. 3.7
. For a
computational mesh with significant non-orthogonality, the corrected
scheme Eq. (3.7
) should be applied to
maintain sufficient accuracy.
, according to
Sec. 3.7
. For a
computational mesh with significant non-orthogonality, the corrected
scheme Eq. (3.7
) should be applied to
maintain sufficient accuracy.
This correction to the pressure Laplacian is
calculated using the current  , which produces an
explicit contribution to the matrix equation. The equation can be
imagined with the explicit correction as an additional term
, which produces an
explicit contribution to the matrix equation. The equation can be
imagined with the explicit correction as an additional term
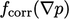 .
.
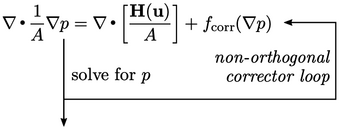
To improve accuracy within each time step
during a transient simulation, 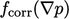 can be recalculated
using the latest
can be recalculated
using the latest 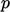 and the equation solved again.
and the equation solved again.
The accuracy can be improved by further iterations, but this is not generally recommended due to the increased computational cost. With the pressure equation encountered twice as part of the PISO loop, and with one corrector on each occasion, the pressure matrix is solved a total of 4 times.
Solving the pressure matrix is costly, so any
reduction in the number of solutions is welcome. Recognising that
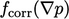 is
updated as part of the PISO iterations anyway, an alternative
solution strategy uses no non-orthogonal correction but adds an
extra PISO loop, solving the pressure equation a total of 3 times.
is
updated as part of the PISO iterations anyway, an alternative
solution strategy uses no non-orthogonal correction but adds an
extra PISO loop, solving the pressure equation a total of 3 times.
Solving the momentum predictor
The transient algorithm on page 385
includes the momentum predictor that
provides an initial solution for 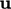 , which is used to
evaluate
, which is used to
evaluate 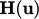 in the pressure equation. The solution for
in the pressure equation. The solution for 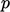 is then
substituted into the momentum corrector which calculates a new
is then
substituted into the momentum corrector which calculates a new
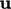 .
.
Since 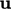 is ultimately recalculated by the momentum
corrector — a momentum equation in explicit form — is it necessary to solve the momentum
predictor at all? The answer is “no”, unless it makes the solution
more convergent which is more likely for high speed flows which are
dominated more by momentum exchanges than mass conservation.
is ultimately recalculated by the momentum
corrector — a momentum equation in explicit form — is it necessary to solve the momentum
predictor at all? The answer is “no”, unless it makes the solution
more convergent which is more likely for high speed flows which are
dominated more by momentum exchanges than mass conservation.
The transient algorithm should therefore include
a simple switch that makes it possible to turn off the momentum
predictor step. The rest of the algorithm remains the same, with
the momentum matrix constructed to provide 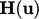 and
and 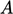 .
.
With this switch included, the momentum predictor is then turned off in a lot of applications, e.g. highly viscous flows. In practice, it is often switched off for more complex flows, e.g. multiphase flows, which are beyond the scope of this book.

