5.8 Accelerating convergence
The Gauss-Seidel method sweeps across cells,
calculating the changes in values of fields, e.g.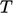 
. Each sweep propagates
the changes in 
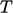through cells in the domain in much the same way that
the flow transports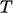 
physically.
The method is therefore remarkably effective, so the scope to accelerate convergence to reduce computational cost is limited. Two options that may reduce cost, relating to mesh numbering, are described in this section.
Symmetric Gauss-Seidel
The Gauss-Seidel method sweeps through
equations in sequence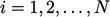 
of cell numbering. The changes in the solution
“flow” in a direction, based on the choice of cell numbering which
may be arbitrary and therefore not optimal.
The symmetric
Gauss-Seidel method follows the standard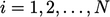 
sequence
initially, known as a forward sweep. For every second sweep,
the sequence is executed in reverse, i.e.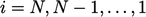 
, known as a
backward sweep.
The change in sweep direction moderates the directional bias of the standard Gauss-Seidel method which may reduce the total iterations for convergence and reduce cost.
Mesh numbering
When a matrix equation is solved in sequence
,
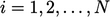values from one row of the equation are substituted in subsequent
equations. Convergence improves if the substitutions are made
quickly, e.g. in the
subsequent 2 or 3 equations rather than in the last equation.
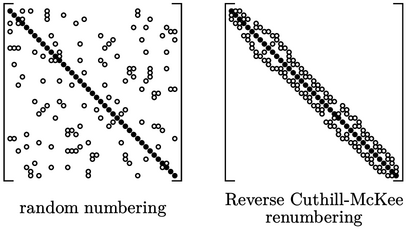
Convergence is therefore affected by the cell numbering which determines the position of non-zero coefficients in the matrix. If the numbering is approaching random, e.g. as a consequence of the mesh generation, convergence is sub-optimal.
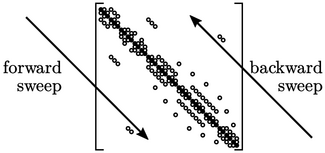
Where this occurs, a method such as reverse Cuthill-McKee2 can be applied to renumber the cells of a mesh to cluster non-zero coefficients around the diagonal, as shows above.
The matrix in Sec. 5.1 is from a mesh generated in a structured manner with ordered indexing along rows of cells. Renumbering a matrix like that generally provides little benefit since it already has many non-zero coefficients clustered around the diagonal.
