5.4 Residual
In Sec. 5.3 , we established a criterion for convergence of the Gauss-Seidel method. We now need a way to estimate a level of convergence to determine when to stop iterating.
The analysis of convergence centred on the
solution error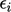 
, introduced in Sec. 5.2
. In practice, 
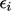cannot be
determined since the exact solution is unknown. Instead the
residual provides a measure
of the accuracy of the solution. The residual vector 
represents the change
to the solution of the equation, required to make 
exact, according
to
 |
(5.10) |
.
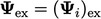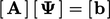is replaced by
,
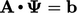equivalent to vector notation with an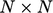 
tensor 
.The vector 
(of size 
) provides
one value per matrix row,
with both positive and negative values. A measure of residual given
by a single value, is
defined as
 |
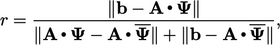(5.11) |
is the matrix norm, calculated as the sum of the magnitude
of each component, e.g.
;
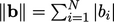the mean value of 
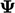over all cells is denoted by 
.
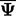The residual 
provides a measure of
error in the solution of
,
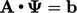rather than the absolute
error 
. It is divided by the norms of 
and 
to reduce its
dependency on the scale of the geometry and solution variable. By
reducing its scale-dependency, 
can be used to compare
the level of error equitably between simulations at different
scales.
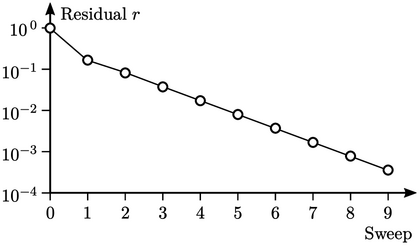
The figure above shows 
calculated from
Eq. (5.11
) following successive sweeps of
the Gauss-Seidel method (starting from the initial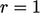 
). The graph uses a
logarithmic vertical scale since the values of 
extend over 4 orders
of magnitude.
Tolerance
CFD software generally provides the following controls to stop the iterative solver:
;
.Sweeping ceases if either tolerance condition is satisfied:
;
or 
, where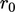 
is the initial residual within the particular
solution step. The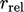 
criterion is often deactivated by setting
,
especially for transient simulations when sufficient accuracy is
required at every solution step.
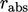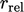