5.16 Preconditioning and asymmetry
The conjugate gradient (CG) method provides a
good basis for a matrix solver in CFD. In theory, it provides an
exact solution in 
steps for a problem with 
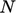values. In practice,
there is an accumulation of rounding errors from finite precision
arithmetic, such that an exact solution is not attained. Problems
are also too large for it to be feasible to run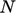 
steps.
CG is instead used as an iterative method, aiming
to get the solution residual within an acceptable tolerance. The
rate of convergence is therefore critical, which can be shown to be
slower for increasing condition
number of the matrix,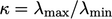 
, where 
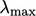and
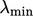are its largest eigenvalues.
In the example with two values, the eigenvalues
correspond to the gradients of the principal axes of the paraboloid
described by the quadratic function. Lower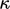 
corresponds to closer
gradients, i.e. to a
rounder “bowl” shape.
The best convergence corresponds to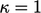 
when
(
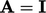is the identity matrix). Preconditioning finds a matrix 
, similar to
,
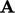which can be inverted and multiplied to the equation as
follows:
 |
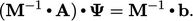(5.35) |
so that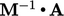 
is closer to 
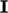than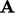 
. Effective methods
for calculating the preconditioner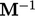 
are:
- diagonal-based incomplete Cholesky (DIC) for
symmetric
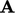; - diagonal-based incomplete LU (DILU) for an
asymmetric
.
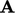Biconjugate gradient stabilised method
The preconditioned CG (PCG) method minimises
the quadratic form which requires that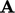 
is symmetric. However,
any equation containing an advection term produces an asymmetric
matrix (see Sec. 5.1
), when PCG is
unsuitable.
The preconditioned biconjugate gradient
(PBiCG) method is designed for asymmetric matrices. It augments the
calculations of residuals and line search directions in the CG
method with a second set of calculations relating to the transpose
matrix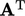 
. The computational cost is approximately 2
the cost of PCG.
The convergence behaviour of PBiCG is somewhat erratic, with large variations in the reduction of the residual between successive iterations. Sometimes the method breaks down and fails.
The preconditioned biconjugate gradient stabilised method (PBiCGStab) is a modification of PBiCG. It is exhibits much smoother convergence and robustness than PBiCG so it is far more preferable for CFD applications.
Recommended CG-based methods are summarised below.
- symmetric: PCG with DIC preconditioning.
- asymmetric: PBiCGStab with DILU preconditioning.
The implementation of preconditioning and CG-based methods can be found in: Barrett R. et al. Templates for the solution of linear systems, available at http://www.netlib.org.
