5.2 Gauss-Seidel method
Finite volume numerics generally uses
iterative methods to solve
each matrix equation. These methods calculate approximate solutions
for 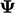 , which become more accurate with successive iterative
solutions.
, which become more accurate with successive iterative
solutions.
Iterative methods are
preferred because they are more efficient than direct methods, which solve a matrix equation exactly.
Gaussian elimination, which is the
numerical basis for direct solution methods, has a computational
cost 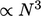 . This is prohibitive for many
sizes of mesh in finite volume CFD.
. This is prohibitive for many
sizes of mesh in finite volume CFD.
Gauss-Seidel1 is a simple, iterative method which is generally effective for solving transport equations such as the example in Sec. 5.1 . The method is illustrated by a sample equation
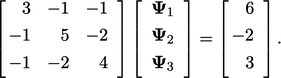 |
(5.2) |
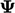 ; b) subtracting the result from the right hand side
(r.h.s.); c) and, dividing by the diagonal coefficient. i.e.:
; b) subtracting the result from the right hand side
(r.h.s.); c) and, dividing by the diagonal coefficient. i.e.:
Starting with, 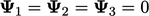 , new values of
, new values of
 are calculated by Eq. (5.3a
), Eq. (5.3b) and
Eq. (5.3c
) in sequence, where the notation
“
are calculated by Eq. (5.3a
), Eq. (5.3b) and
Eq. (5.3c
) in sequence, where the notation
“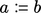 ”
denotes “
”
denotes “ is assigned the value of
is assigned the value of 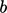 ”.
”.
The first solution of Eq. (5.3a) is
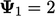 .
The updated
.
The updated 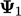 is substituted in Eq. (5.3b), whose
solution is
is substituted in Eq. (5.3b), whose
solution is  . Both updated values are substituted in
Eq. (5.3c
) to give
. Both updated values are substituted in
Eq. (5.3c
) to give 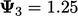 .
.
The process is then repeated and through successive sweeps over the equations the solution converges as shown below.
| Variable | Start | Sweep 1 | …2 | …3 | …4 |
|
|
|
|
|
|
|
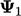 |
0.0000 | 2.0000 | 2.4167 | 2.7431 | 2.8821 |
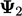 |
0.0000 | 0.0000 | 0.5833 | 0.8069 | 0.9121 |
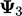 |
0.0000 | 1.2500 | 1.6458 | 1.8392 | 1.9266 |
| Variable | Sweep 5 | …6 | …7 | …8 | …9 |
|
|
|
|
|
|
|
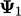 |
2.9462 | 2.9755 | 2.9888 | 2.9949 | 2.9977 |
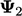 |
0.9599 | 0.9817 | 0.9916 | 0.9962 | 0.9983 |
 |
1.9665 | 1.9847 | 1.9930 | 1.9968 | 1.9985 |
The error is 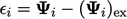 , i.e.
the difference between the approximate and exact values
, i.e.
the difference between the approximate and exact values  ,
, 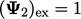 and
and
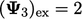 .
After 9 sweeps
.
After 9 sweeps 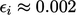 for all variables, i.e. within 0.2% of the exact
solution.
for all variables, i.e. within 0.2% of the exact
solution.
In summary, the Gauss-Seidel method is the
following sequence of calculations for 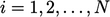 , repeated until
convergence:
, repeated until
convergence:
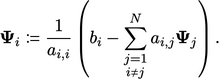 |
(5.4) |
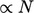 , making it
practical for simulations with large meshes that often occur in
finite volume CFD.
, making it
practical for simulations with large meshes that often occur in
finite volume CFD.
Convergence of the method, and convergence measures for iterative methods in general, are discussed in the following sections.


