5.10 Pressure-velocity coupling
The previous section combined equations for
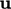and 
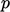, governing momentum and mass conservation, in a sequential
solution.
The algorithms used to couple these equations, in
a manner which is convergent, uses the following notation to
describe terms in the momentum equation, e.g. Eq. (2.67
),
excluding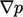 
 |
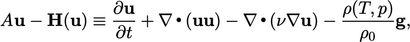(5.16) |
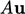is a linear term in 
;
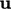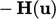is a function of 
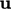and other
sources.
Momentum corrector
A momentum corrector equation is formed by expressing the momentum equation, e.g. Eq. (2.67 ) in terms of the notation of Eq. (5.16 ), and rearranging to give
 |
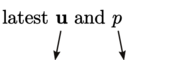
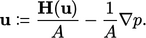(5.17) |
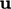, based on current
values of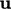 
and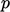 
substituted on the r.h.s. In other words,
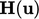and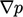 
are calculated explicitly.
In the algorithms described in the following
sections, 
is chosen to be the extracted diagonal coefficients
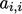
of
the matrix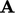 
corresponding to the momentum terms in
Eq. (5.16
).
The split between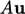 
and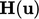 
is shown above. As
a matrix with diagonal components only,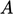 
has one value per cell
so can be represented as a scalar field. Setting 
to be the diagonal
coefficients is a natural choice for implicit treatment of
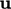within the coupling algorithm.
Flux corrector
A flux
corrector equation follows from Eq. (5.17)
by interpolating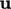 
to cell faces and evaluating 
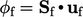according to
 |
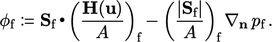(5.18) |
Pressure equation
A pressure
equation is then created by substituting fluxes 
from
Eq. (5.18
) into the mass
conservation Eq. (2.46
) in discrete form
.
The resulting expression is equivalent to a discretised pressure
equation, with coefficients containing 
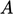and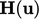 
,
 |
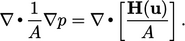(5.19) |
