5.9 Systems of equations
Most CFD calculations involve solving a system of equations that represent the physics of the problem. For example, laminar flow by natural convection can be represented by the equations introduced in Sec. 2.20 , reproduced below.
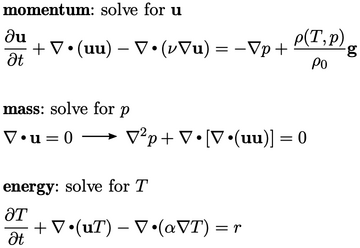
The system provides 3 equations (1 vector, 2
scalar) which can be solved for 3 unknowns,  ,
, 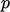 and
and 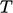 .
.
As discussed in Sec. 3.4
, the finite volume method
solves an individual matrix equation for each variable,
e.g.  for
for 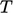 . The vector
equation for
. The vector
equation for 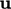 is decoupled into 3 matrix equations for individual
components, i.e.
is decoupled into 3 matrix equations for individual
components, i.e.
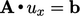 ,
,
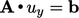 and
and 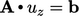 .
.
Each individual matrix equation for one solution
variable, e.g. 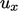 , incorporates
terms from other variables, e.g.
, incorporates
terms from other variables, e.g. 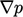 , into the source
vector
, into the source
vector 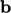 . The contribution to
. The contribution to 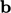 is calculated using
current values of the respective variables. Systems of equations
are thereby solved by successive
substitution of solved variables into the source vectors of
subsequent equations.
is calculated using
current values of the respective variables. Systems of equations
are thereby solved by successive
substitution of solved variables into the source vectors of
subsequent equations.
An iterative solution for a single equation, like
the one in Sec. 5.7
, can be extended to a
system of equations. Time 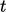 is incremented by
is incremented by 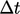 and equations are
solved in sequence, before returning to start the next time step
with the increment of
and equations are
solved in sequence, before returning to start the next time step
with the increment of 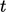 .
.
The substitutions in the momentum and pressure
equations are particularly important, culminating in corrections to 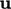 and the advective
flux
and the advective
flux 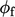 , discussed in
Sec. 5.10
.
, discussed in
Sec. 5.10
.
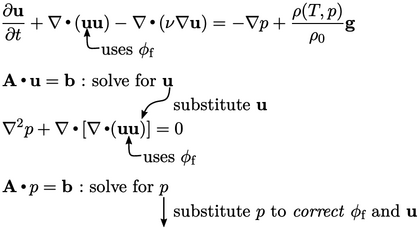
At the start of any time step the current
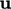 becomes
becomes 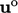 for the discretisation of the
for the discretisation of the 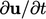 term in the momentum
equation. The advection term
term in the momentum
equation. The advection term  is discretised by
Eq. (3.8
), treating one
is discretised by
Eq. (3.8
), treating one
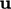 as
flux
as
flux 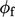 and the other as the advected quantity.
and the other as the advected quantity.
The equation is solved for  . The new solution for
. The new solution for
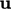 is
substituted into the
is
substituted into the 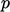 equation which is solved for
equation which is solved for 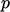 . The new solution
for
. The new solution
for  is then used to correct
is then used to correct 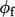 in order to help
enforce the mass conservation constraint
in order to help
enforce the mass conservation constraint 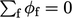 (
(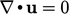 ).
).
Before the current solution step is completed,
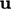 is
also corrected to reduce the error in the discretisation of
is
also corrected to reduce the error in the discretisation of
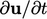 when it then becomes
when it then becomes 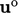 in the following solution step. The correction
also provides a better “initial guess”
in the following solution step. The correction
also provides a better “initial guess” 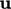 for the matrix
solution of the next momentum equation, which reduces the solution
time.
for the matrix
solution of the next momentum equation, which reduces the solution
time.

