5.5 Diagonal dominance
Let us return to the transport equation in Sec. 5.1
 |
(5.12) |
If the Gauss-Seidel method is applied to solve the equation, a convergent solution is only guaranteed if the diagonal dominance condition of Sec. 5.3 is satisfied.
The contributions to the diagonal and off-diagonal coefficients are summarised below for each term in the equation.
The Laplacian term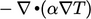 
(note the sign), is
discretised by Eq. (3.2
) and
Eq. (3.5
), providing a positive
contribution to the diagonal coefficient (relating to 
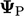) equal to the sum
of the magnitude of negative off-diagonal coefficients (for
).
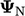The contribution from the advection term
,
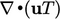described by Eq. (3.8
), is
demonstrated above using the linear interpolation scheme of
Eq. (3.4
). The sign of
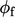depends on whether the flux in incoming or outgoing from the cell.
Some contributions to off-diagonal coefficients are thus negative and
some positive, with the diagonal contribution tending to zero as
the mesh becomes more regular and flow becomes more uniform.
Advection with linear interpolation maintains diagonal equality while its positive off-diagonal contributions offset the negative contributions from the Laplacian term.
But once the advection contributions exceed the
magnitude of the Laplacian contributions, diagonal equality is
not achieved. This occurs
when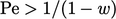 
(= 2 for a regular mesh), where the “numerical” Péclet
number
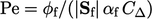is
specified at cell faces from its definition in Sec. 2.21
with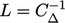 
.
Diagonal equality is achieved with upwind interpolation and any scheme that provides an explicit correction on upwind, e.g. linear upwind. This is conditional on mass conservation being satisfied, as discussed in Sec. 3.22 . If mass is not conserved, the bounded advection scheme, described in that section, is required to ensure diagonal equality.
The time derivative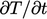 
increases the diagonal
coefficient only, so promotes diagonal dominance. Notably, the
diagonal contribution of 
from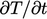 
becomes larger than
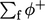from advection with upwind when 
.
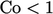In summary, diagonal dominance is not guaranteed due to the contribution of the advection term.
