Notes on Computational Fluid Dynamics: General Principles

5.6 Under-relaxation

Sec. 5.5 concludes that the matrix of a typical transport equation is not guaranteed to be diagonally dominant. Some action may therefore be required to ensure a convergent solution.

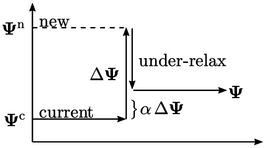
Under-relaxation is a general method used to improve solution convergence by limiting the amount a variable changes during a solution step.

During a solution step, assume a single value of a field 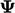in one cell changes from its current value 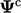to the new value 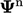. Under-relaxation would limit the change 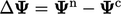by a fraction 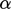, , 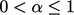so that the value taken from that solution step is

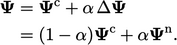(5.13)

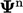In some situations, Eq. (5.13 ) is applied after a solution step. This simple approach is known as field under-relaxation, which has one notable disadvantage that it requires additional storage of the intermediate field in computer memory.

When a solution step involves solving a matrix equation, the new values 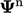come from an iterative method like Gauss-Seidel. Combining the under-relaxation of Eq. (5.13 ) with the Gauss-Seidel calculation of Eq. (5.4 ) gives:

(5.14)

Rearranging Eq. (5.14 ) gives the following relation:

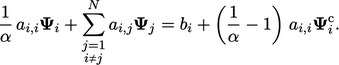(5.15)

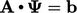Equation 5.15 is simply the matrix equation modified by:

• increasing the diagonal coefficients 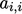by division by ;
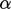• multiplying the difference between the new and original 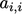coefficients by the current and adding it to the source .

Modifying the matrix equation this way, known as equation under-relaxation, provides an alternative to Eq. (5.13 ) for under-relaxing a solution of , without the temporary storage of .

Ensuring diagonal dominance

The modification to 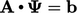expressed by Eq. (5.15 ) inspires a strategy to ensure diagonal dominance of the matrix as follows.

Each diagonal coefficient which does not satisfy Eq. (5.9 ) is increased until it is diagonally equal. The change to the coefficient is multiplied by the current 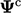and added to .

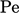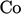This approach to ensure diagonal dominance is effective since it only modifies matrix coefficients where necessary. Otherwise, if the discretisation schemes, and and are favourable, then no changes to the matrix are necessary.