7.15 Summary of turbulence modelling
- The
 model solves transport equations for
turbulent kinetic energy
model solves transport equations for
turbulent kinetic energy 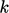 and dissipation rate
and dissipation rate  , Sec. 7.1
.
, Sec. 7.1
. - It is the original of a family of two-equation
models, which ultimately provide
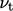 to calculate the
turbulent stresses.
to calculate the
turbulent stresses. - Initial and inlet values for
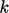 and
and 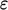 must be specified,
which can be calculated from turbulent intensity
must be specified,
which can be calculated from turbulent intensity 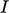 and mixing length
scale
and mixing length
scale 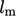 , respectively, Sec. 7.2
.
, respectively, Sec. 7.2
.  and
and 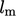 are often estimated using functions that fit
experimental data for fully developed turbulent flow,
Sec. 7.3
.
are often estimated using functions that fit
experimental data for fully developed turbulent flow,
Sec. 7.3
.- The
 models replace
models replace 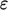 by specific dissipation
rate
by specific dissipation
rate 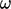 , with equivalent expressions for initial and inlet values,
Sec. 7.10
.
, with equivalent expressions for initial and inlet values,
Sec. 7.10
. - The two “standard”
 models today are the
models today are the
 SST model and
SST model and  2006 model, Sec. 7.11
.
2006 model, Sec. 7.11
. - Models can provide a turbulent conductivity
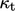 to
calculate the turbulent heat flux for thermal problems,
Sec. 7.12
.
to
calculate the turbulent heat flux for thermal problems,
Sec. 7.12
.
Turbulent boundary layers
- Turbulent boundary layers include a thin viscous sub-layer adjacent to the boundary with a linear velocity profile and, further from the boundary, the inertial sub-layer with a log law profile, Sec. 7.4 .
- Profiles in temperature are similar to those for velocity, with equivalent linear and log law relationships, Sec. 7.13 .
- Very thin cells are generally needed to resolve
the viscous sub-layer to calculate the velocity gradient
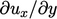 at
the wall accurately, Sec. 7.5
.
at
the wall accurately, Sec. 7.5
. - Such thin cells within the boundary layer region can increase the mesh to a size which is prohibitively costly to run.
Wall functions
- Wall functions permit much larger cells near the wall, by exploiting the universal character of the velocity distribution.
- The functions increase
 at the wall to
compensate for the under-prediction of
at the wall to
compensate for the under-prediction of 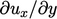 with larger cells, to
improve the prediction of the wall shear stress, Sec. 7.5
.
with larger cells, to
improve the prediction of the wall shear stress, Sec. 7.5
. - Thermal wall functions similarly increase
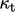 at
the wall to compensate for the under-prediction of
at
the wall to compensate for the under-prediction of 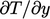 , in order to
improve the prediction of the wall heat flux, Sec. 7.14
.
, in order to
improve the prediction of the wall heat flux, Sec. 7.14
. - Standard wall functions make no adjustment to
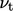 when the near wall cell centre falls below the transition within a
buffer layer, Sec. 7.5
.
when the near wall cell centre falls below the transition within a
buffer layer, Sec. 7.5
. - Other models include a continuous function of
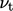 through the viscous sub-layer to the wall and adjustments for
surface roughness, Sec. 7.6
.
through the viscous sub-layer to the wall and adjustments for
surface roughness, Sec. 7.6
. - Boundary conditions for turbulence fields with wall functions are based on observed profiles of those fields, Sec. 7.7 .
Models with resolved boundary layers
- Turbulence models must predict the universal character of boundary layers when the viscous sub-layer is resolved with sufficiently thin cells, Sec. 7.8 .
- Models like the Launder-Sharma
 include source
terms and damping functions to improve the predictions and to
simplify boundary conditions, Sec. 7.9
.
include source
terms and damping functions to improve the predictions and to
simplify boundary conditions, Sec. 7.9
.
Notes on CFD: General Principles - 7.15 Summary of turbulence modelling

